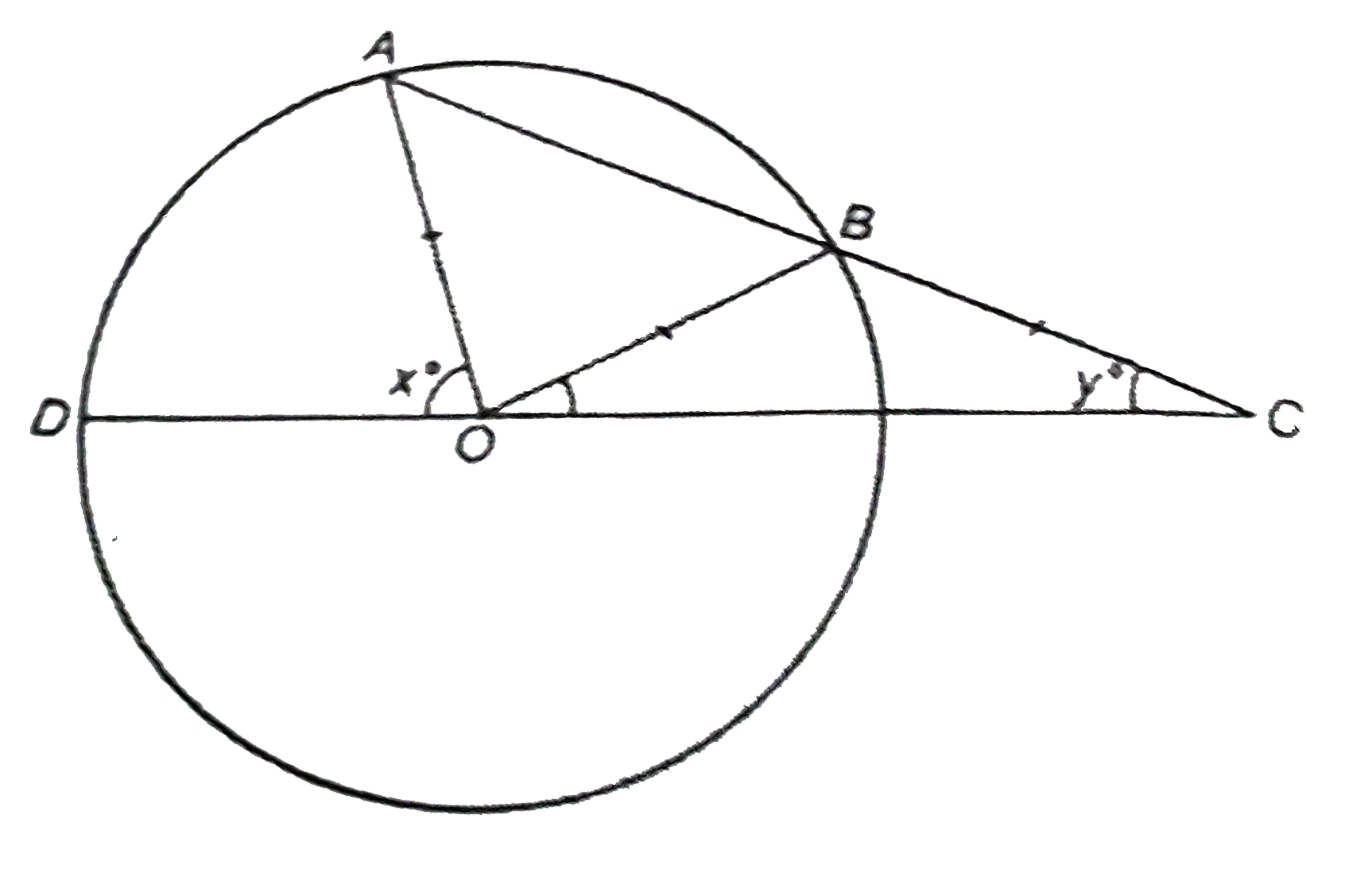
AB is the chord of a circle with centreO. AB is produced to C, such that BC =OB, CO is joined and produced to meet the circle in D.
If ∠ACD=Y∘ and ∠AOD=x∘, Prove that x=3y.
Given : AB is a chord of a with centreO. Also, BO=BC.CO is joined produced to meet the circle at D.
To prove : x=3y
Proof : Since BC=OB (given)
∴∠OCB=∠BOC=Y∘ (angles opposite to equal sides are equal)
∴∠ABO=∠BOC+∠OCB (exterior angle circle)
⇒∠ABO=y+y=2y
Now, OA=OB (radii of same circle)
∴∠OAB=∠ABO (angles opposite to equal sidse are equal )
2y
Similar Questions
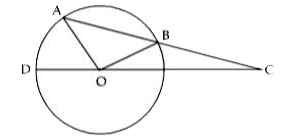
In the figure given below, AB is the chord of a circle with centre O. AB is extended to C such that BC = OB. The straight line Co is produced to meet the circle at D. If ACD = y and AOD = x, such that x = ky, then the value of k is.
View SolutionIn a triangle ABC, if AB=AC and AB is produced to D such that BD=BC, find ∠ACD : ∠ADC
View Solution
Knowledge Check
- Question 1 - Select One
AB is a chord in a circle with centre O. AB is produced to C such that BC is equal to the radius of the circle. C is joined to O and produced to meet the circle at D. If ∠ACD=32∘, then the measure of ∠AOD is .......
A48∘B96∘C108∘D80∘ - Question 2 - Select One
AB is a diameter of a circle with centre O. CD is a chord equal to the radius of the circle. AC and BD are produced to meet at P. Then the measure of ∠APB is:
A120∘B30∘C60∘D90∘ - Question 3 - Select One
AB is a diameter of the circle with centre O and chord CD is equal to radius OC (fig). AC and BD proudced meet at P. Prove that ∠CPD=60∘.
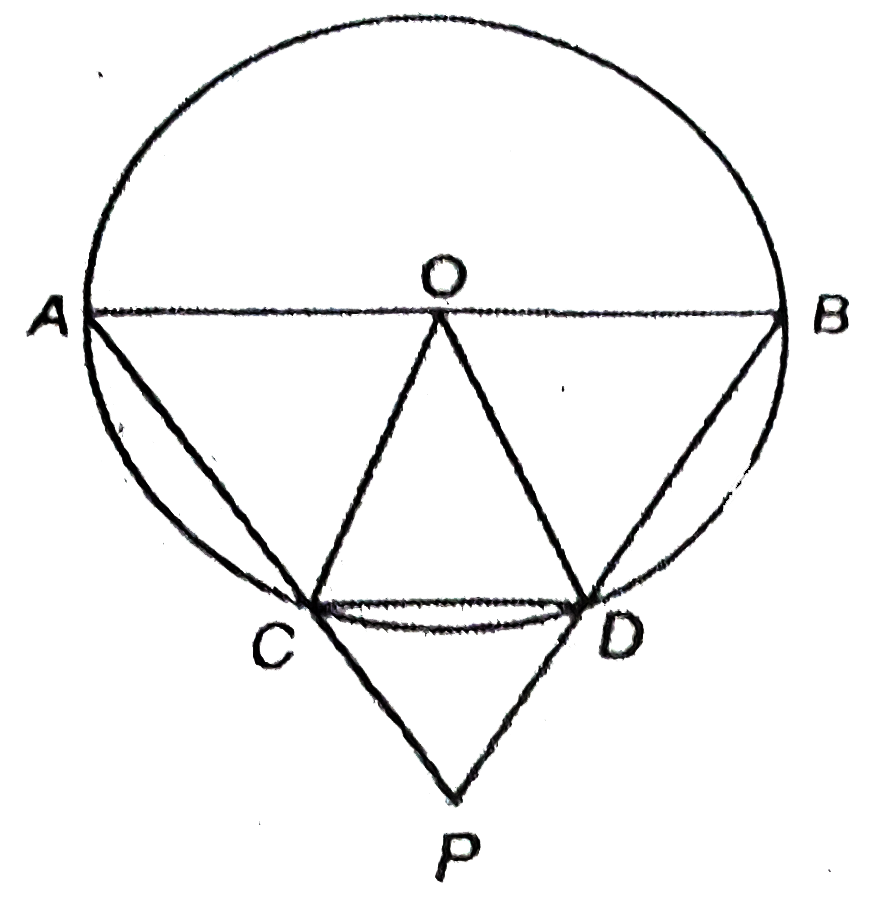A60∘B30∘C90∘D160∘
ABandCD are equal chords of a circle whose centre is O, when produced these chords meet at E,Prove that EB=ED.
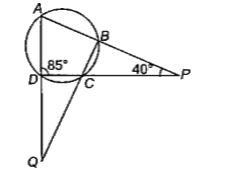
View SolutionThe sides AB and CD of a cyclic quadrilateral ABCD are produced to meet at P. The sides AD and BC are produced to meet at Q. If ∠ADC=85∘and∠BPC=40∘, then ∠BAD is equal to
View SolutionIn a circle with centre O, AOC is a diameter of the circle, BD is a chord and OB and CD are joined. If ∠AOB =130∘, then ∠BDC is equal to
View SolutionAB is the diameter of a circle with centre O. The tangent at a point C on the circle meets AB produced at Q. If ∠CAB=42∘, then what is the measure of ∠CQA?
AB एक वृत्त का व्यास है जिसका केंद्र O है | वत्त पर स्थित एक बिंदु C से गुजरने वाली स्पर्श रेखा AB से Q पर मिलती है | यदि ∠CAB=42∘ है, तो ∠CQA का मान क्या होगा ?View SolutionAB is the chord of a circle with centre O and DOC is a line segment originating from a point D on the circle and intersecting AB produced at C such that BC = OD. If ∠BCD=20∘, then ∠AOD= ?
View Solution