In the given figure AB is the diameter and AC is the chord of a circle such that ∠BAC=30∘. The tangent at C intersects AB produced at D. Prove that :BC=BD.
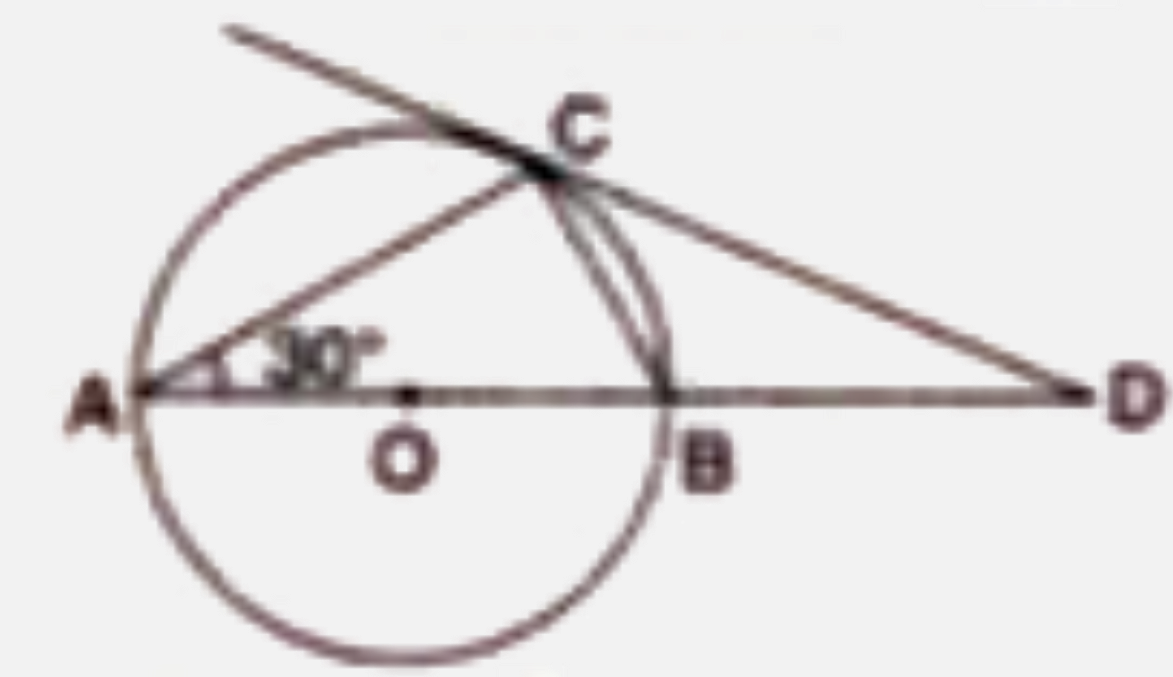
The correct Answer is:BC=BD
Step by step video & image solution for In the given figure AB is the diameter and AC is the chord of a circle such that /_BAC=30^(@). The tangent at C intersects AB produced at D. Prove that :BC=BD. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TANGENTS AND INTERSECTING CHORDSBOOK - ICSECHAPTER - TANGENTS AND INTERSECTING CHORDSEXERCISE - EXERCISE 18(A)
24 Videos
- TANGENTS AND INTERSECTING CHORDSBOOK - ICSECHAPTER - TANGENTS AND INTERSECTING CHORDSEXERCISE - EXERCISE 18 (B)
18 Videos
- SPECIMEN QUESTION PAPER (MATHEMATICS)BOOK - ICSECHAPTER - SPECIMEN QUESTION PAPER (MATHEMATICS)EXERCISE - Section C
12 Videos
- TRIGONOMETRICAL IDENTITIESBOOK - ICSECHAPTER - TRIGONOMETRICAL IDENTITIESEXERCISE - QUESTIONS
22 Videos
Similar Questions
AB is the diameter and AC is a chord of a circle with centre O such that angle BAC=30∘. The tangent to the circle at C intersects AB produced in D. Show that BC=BD.
View SolutionAB is a diameter of a circle and AC is its chord such that ∠BAC=30∘. If the tengent at C intersects AB extended at D, then BC=BD.
View SolutionAB is a diameter of a circle and AC is its chord such that ∠BAC=30∘. If the tengent at C intersects AB extended at D, then BC=BD.
View SolutionIn the given figure AB, BC, BD cannot be in

View SolutionIn the given figure AC = BD, prove that AB = CD.

View SolutionIn the adjoinig figure, AB is a diameter of the circle, CD is a chord equal to the radius of the circle. AC and BD when extended intersect at a point E. Prove that ∠AEB=60∘.

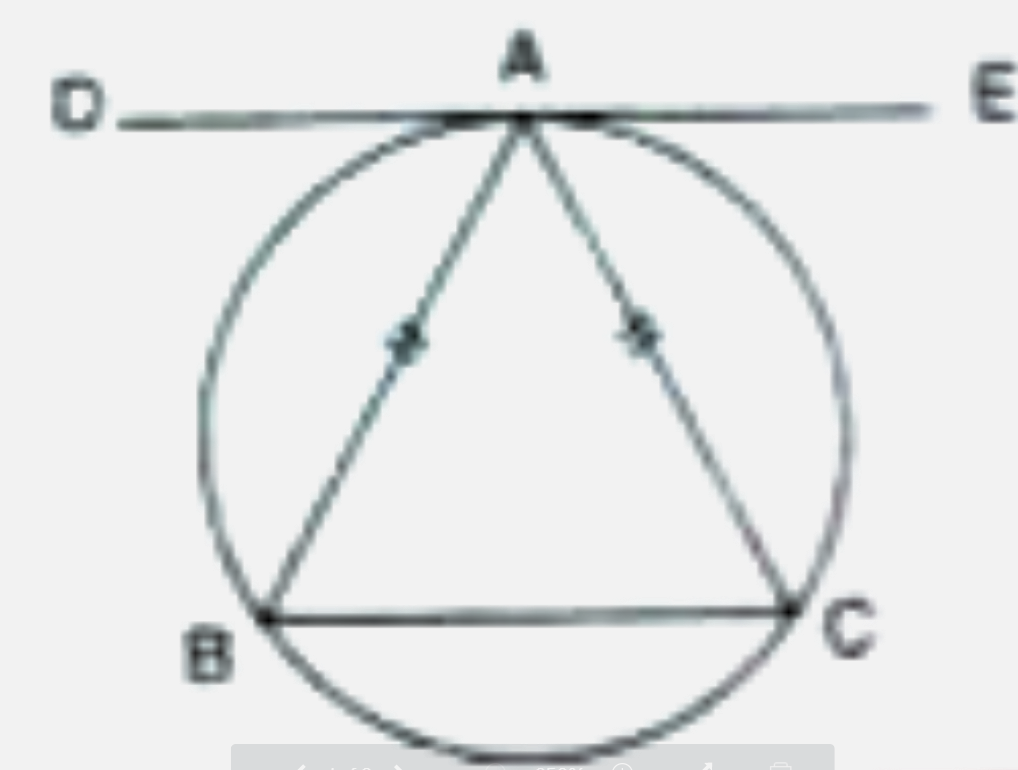
View SolutionThe given figure shows an isosceles triangle ABC inscribed in a circle such that AB=AC. If DAE is a tangent to the circle at point A, prove that DE is parallel to BC.
View SolutionAB is a diameter of a circle. CD is a chord parallel to AB and 2CD=AB. The tangent at B meets the line AC produced at E then AE is equal to -
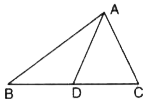
View SolutionIn the given figures, AB > AC and D is any point on BC.
Prove that : AB >AD.
View SolutionIn the given figure, ∠ABC=90∘ and BC is diameter of the given circle. Show that:
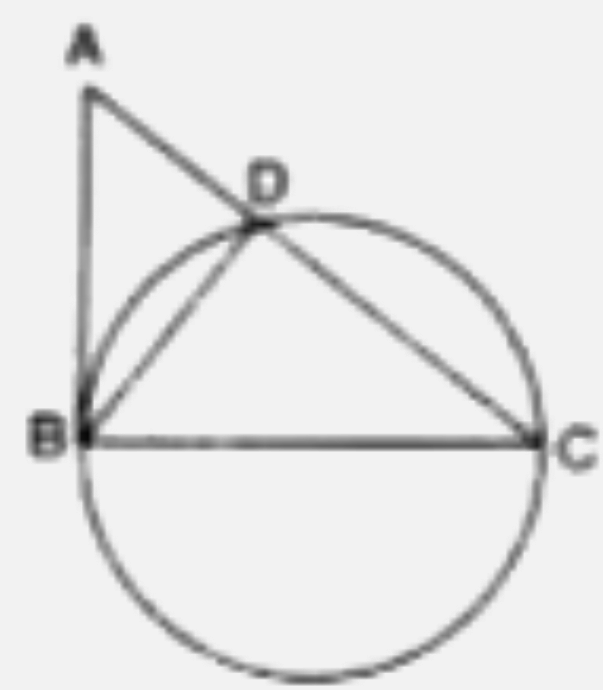
AC×AD=AB2
View Solution
