ABC is a right triangle, right angled at C and AB=√2BC. Then, find ∠ABC.
The correct Answer is:45∘
To solve the problem, we will follow these steps:
Step 1: Understand the Triangle
We have a right triangle ABC, where angle C is the right angle. We know that AB=√2⋅BC.
Step 2: Assign Variables
Let:
- BC=x (the length of side BC)
- Then, AB=√2⋅x (the length of side AB)
Step 3: Use the Pythagorean Theorem
In a right triangle, the Pythagorean theorem states that:
AB2=AC2+BC2
Substituting the known lengths:
(√2⋅x)2=AC2+x2
This simplifies to:
2x2=AC2+x2
Step 4: Rearranging the Equation
Now, we can rearrange the equation to find AC2:
AC2=2x2−x2
AC2=x2
Taking the square root of both sides gives:
AC=x
Step 5: Find the Angles Using Trigonometric Ratios
Now we need to find angle ABC, which we will denote as θ.
Using the cosine ratio:
cos(θ)=BCAB
Substituting the values we have:
cos(θ)=x√2⋅x
This simplifies to:
cos(θ)=1√2
Step 6: Determine the Angle
We know that:
cos(45∘)=1√2
Thus:
θ=45∘
Final Answer
The angle ABC is 45∘.
---
We have a right triangle ABC, where angle C is the right angle. We know that AB=√2⋅BC.
Let:
- BC=x (the length of side BC)
- Then, AB=√2⋅x (the length of side AB)
In a right triangle, the Pythagorean theorem states that:
AB2=AC2+BC2
Substituting the known lengths:
(√2⋅x)2=AC2+x2
This simplifies to:
2x2=AC2+x2
Now, we can rearrange the equation to find AC2:
AC2=2x2−x2
AC2=x2
Taking the square root of both sides gives:
AC=x
Now we need to find angle ABC, which we will denote as θ.
cos(θ)=BCAB
Substituting the values we have:
cos(θ)=x√2⋅x
This simplifies to:
cos(θ)=1√2
We know that:
cos(45∘)=1√2
Thus:
θ=45∘
The angle ABC is 45∘.
Topper's Solved these Questions
- SAMPLE PAPER 8BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 8EXERCISE - PART-A (SECTION-II)
20 Videos
- SAMPLE PAPER 8BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 8EXERCISE - PART-B (SECTION-III)
9 Videos
- SAMPLE PAPER 8BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 8EXERCISE - SECTION-C
10 Videos
- SAMPLE PAPER 7BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 7EXERCISE - PART - B (SECTION - V)
8 Videos
- SAMPLE PAPER 9BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 9EXERCISE - SECTION C
10 Videos
Similar Questions
Knowledge Check
ABC is a right-angled triangle, right angled at A and AD is the altitude on BC. If AB : AC= 3:4, what is the ratio BD:DC?
A3:4B9:16C2:3D1:2ABC is right angled triangle, right angled at C . D is the midpoint of BC. Then , tanθtanϕ =
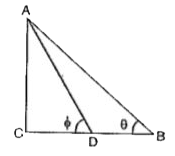 A1B1√2C12D2
A1B1√2C12D2
In a triangle ABC, right angled at B, then
View SolutionABC is a right triangle right-angled at CandAC=√3BC . Prove that ∠ABC=600.
View SolutionABC is a triangle right angled at C. If AB=25cmandAC=7cm, find BC.
View Solution
△ABC is a right triangle, right angled at B. ∠C is a given acute angle. So side BC is base, a side AB is altitude and side AC is hypotenuse for given acute angle C. The ratio BCAC is equal to ________
View SolutionABC is a right triangle right-angled at A and AD⊥BC . Then, BDDC= (ABAC)2 (b) ABAC (c) (ABAD)2 (d) ABAD
View SolutionABC is a right triangle, right angled at C. If A=300andAB=40 units, find the remaining two sides and ∠BofABC.
View Solution
