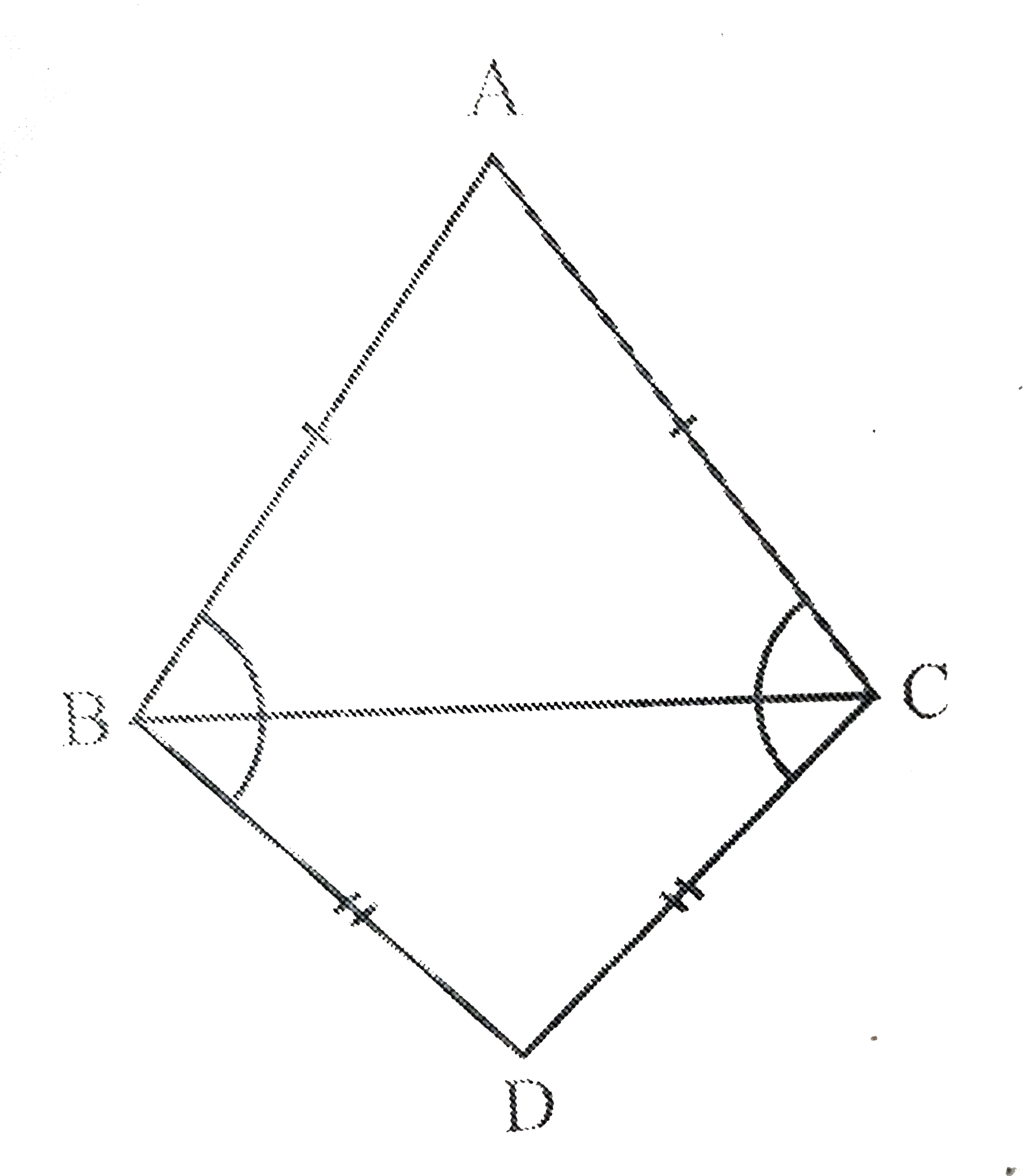
ABC is an isosceles triangle in which . Side BA is produced to D such that (see Fig. 7.34). Show that is a right angle.
In isosceles triangle ABC,
(Given)
(Angles opposite to equal sides of a triangle are equal)
Let be x. ----------- (1)
In ,
(Since, AB = AD)
(Angles opposite to equal sides of a triangle are equal)
Let be y. ----------- (2)
Thus, ----------- (3)
In ,
(Angle sum property of a triangle)
Substituting the values we get,
[From equation (1), (2) and (3)]
[From equation(3)]
∴
Topper's Solved these Questions
Similar Questions
ABC is an isosceles triangle with AB=AC. Side BA is produced to D such that AB=AD. Prove that ∠BCD is a right angle.
View SolutionIn an isosceles triangle ABC with AB=AC, D and E are points on BCsuch that BE=CD(see Fig. 7.29). Show that AD=AE
View SolutionD is a point on side BC of ΔABCsuch that AD = AC(see Fig. 7.47).Show that AB > AD.
View SolutionABC is an isosceles triangle with AB=AC and D is a point on AC such that BC2=ACxCD. Prove that BD=BC
View SolutionABC is an isosceles triangle with AB=AC and D is a point on AC such that BC2=ACXCD. Prove that BD=BC.
View SolutionABC is an isosceles triangle in which AB=AC. AD bisects exterior angle PAC and CD∣∣AB. Show that(i) ∠DAC=∠BCA and (ii) ABCD is a parallelogram.
View SolutionIn a triangle ABC, if AB=AC and AB is produced to D such that BD=BC, find ∠ACD : ∠ADC
View SolutionABC and DBC are two isosceles triangles on the same base BC (see Fig. 7.33). Show that∠ABD =∠ACD
 View Solution
View SolutionABC is a right angled triangle in which ∠A=900and AB=AC. Find ∠B and ∠C
View SolutionIf ABC is an isosceles triangle and D is a point on BC such that AD⊥BC then,
View Solution

