ABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively (see Fig. 7.31). Show that these altitudes are equal.

(##IX07_E0203_s01##)
Given
AB=AC,
BE and CF are altitudes
To Prove
BE=CF
Proof
From ΔAEB and ΔAFC,
∠E=∠F
∠A=∠A
AB=AC
∴ΔAEB≅ΔAFC [A.A.S congruency]
BE=CF
Topper's Solved these Questions
Similar Questions
ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see Fig. 7.32). Show that
(i) ΔABE≅ΔACF
(ii) AB = AC, i.e., ABC is an isosceles triangle.
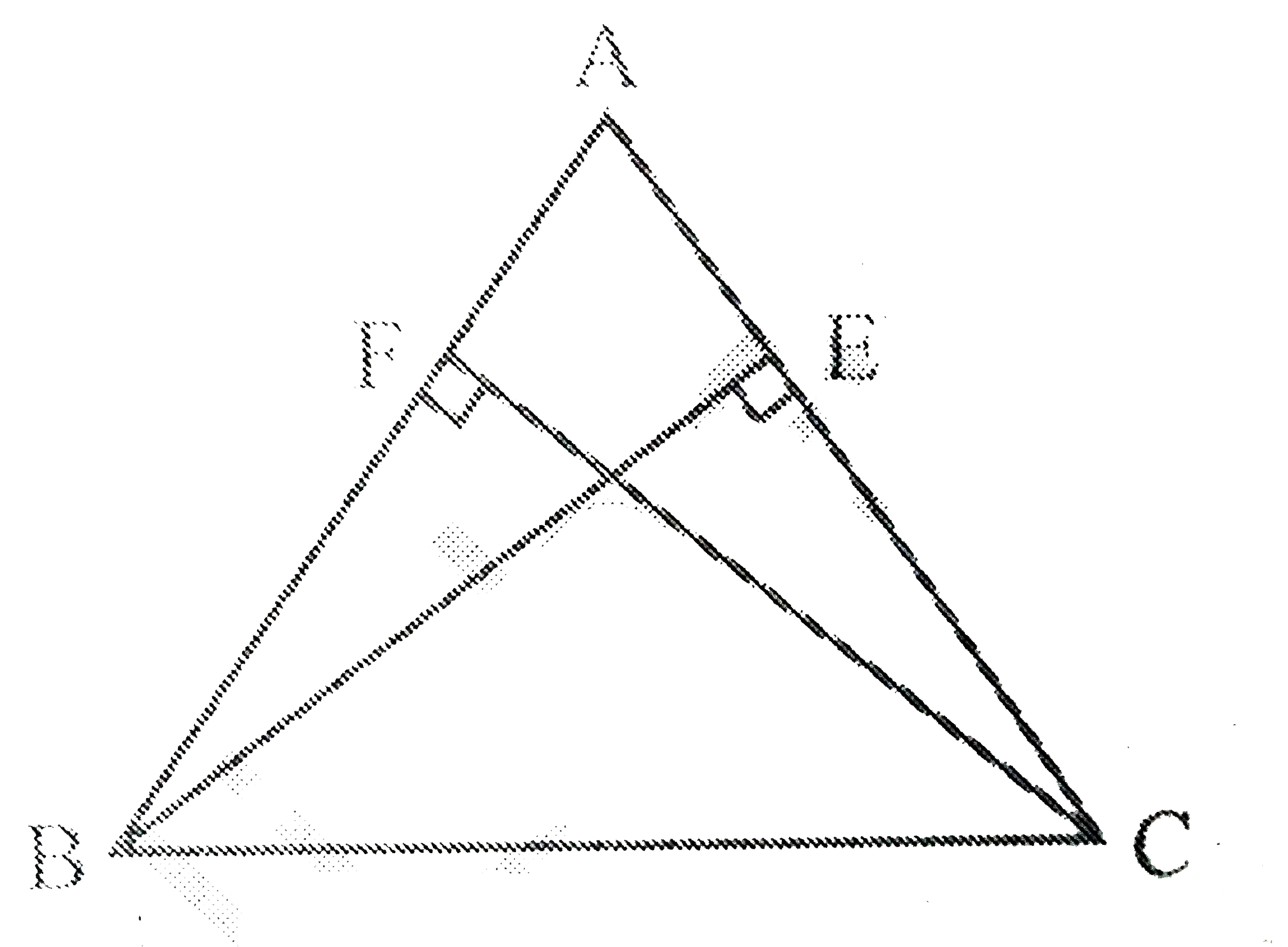
View SolutionABC is an isosceles triangle in which AB= AC . Side BA is produced to D such that AD = AB (see Fig. 7.34). Show that ∠BCD is a right angle.
View SolutionABC is an isosceles triangle with AB =AC and BD,CE are its two medians. Show that BD=CE .
View SolutionIn an isosceles triangle, prove that the angles opposite to equal sides are equal.
View SolutionE and F are respectively the mid-points of equal sides AB and AC of ΔABC(see Fig. 7.28). Show that BF = C E.
View SolutionIn an isosceles triangle ABC with AB=AC, D and E are points on BCsuch that BE=CD(see Fig. 7.29). Show that AD=AE
View SolutionShow that in an isosceles triangle, angles opposite to equal sides are equal.
View SolutionAD and BC are equal perpendiculars to a line segment AB (see Fig. 7.18). Show that CD bisects AB.

View SolutionIn ΔABC,AB=AC.D,Eand F are mid-points of the sides BC, CA and AB respectively . Show that :
AD is perpendicular to EF.
View SolutionThe sides AB and AC are equal of an isosceles triangle ABC. D E and F are the mid-points of sides BC, CA and AB respectively. Prove that:
(i) Line segment AD is perpedicular to line segment EF.
(ii) Line segment AD bisects the line segment EF.
View Solution
