ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see Fig. 7.32). Show that
(i) ΔABE≅ΔACF
(ii) AB = AC, i.e., ABC is an isosceles triangle.
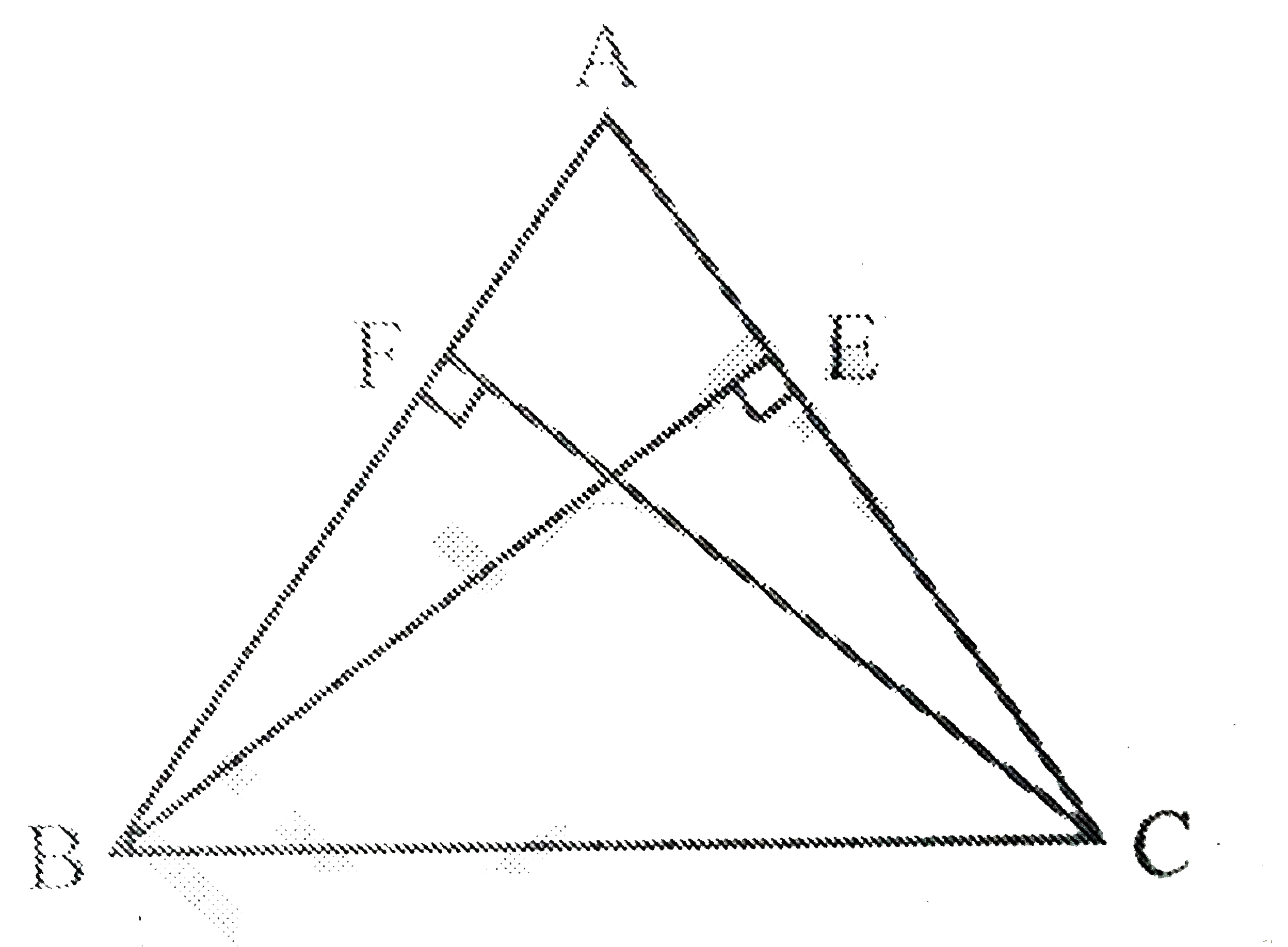
(##IX07_E0204_s01##)
Given
Altitudes are BE and CF to sides AC and AB are equal
To Prove
(i)ΔABE≅ΔACF
(ii)AB=AC
Proof
(i)ΔABE≅ΔACF
In ΔABF and ΔACF,
∠E=∠F [Each 90∘ angle]
∠A=∠A [common angle]
AB=AC [given] S
∴ΔAEB≅ΔAFC [A.A.S]
(ii) AB=AC [C.P.C.T]
Hence Proved
Topper's Solved these Questions
Similar Questions
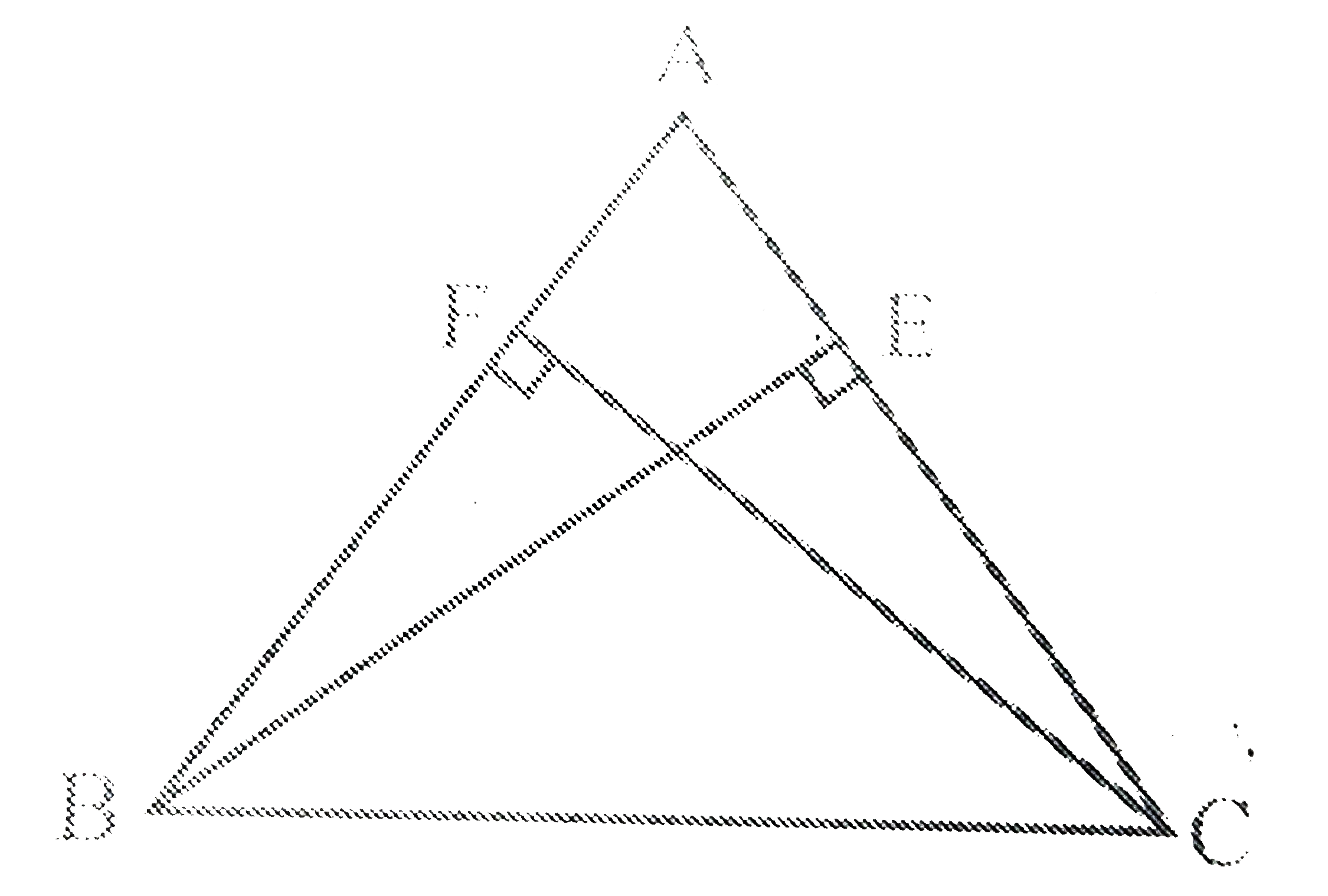
ABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively (see Fig. 7.31). Show that these altitudes are equal.
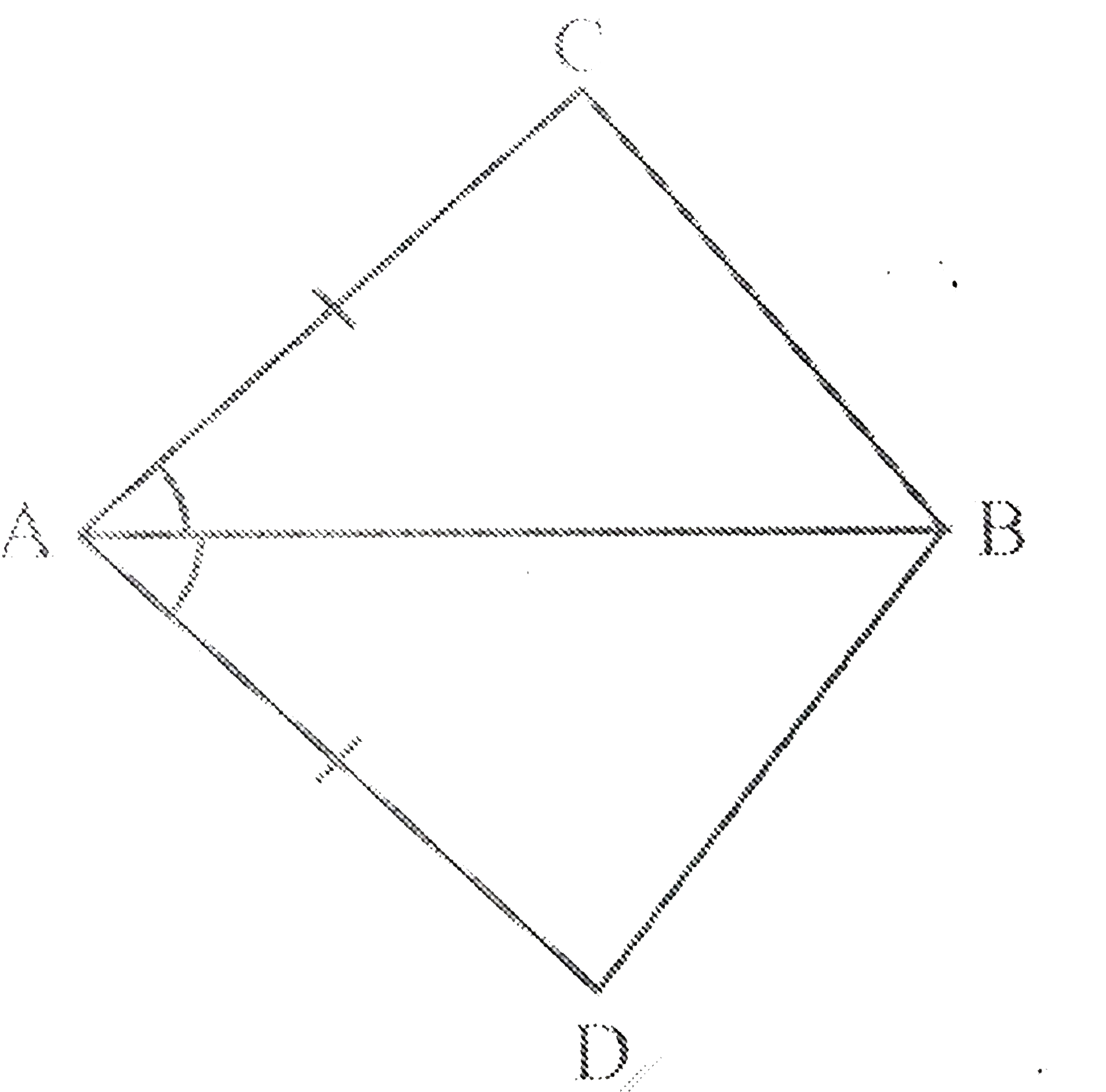
View SolutionIn quadrilateral ACBD, AC = ADand AB bisects ∠A(see Fig. 7.16). Show that ΔABC≅ΔABD
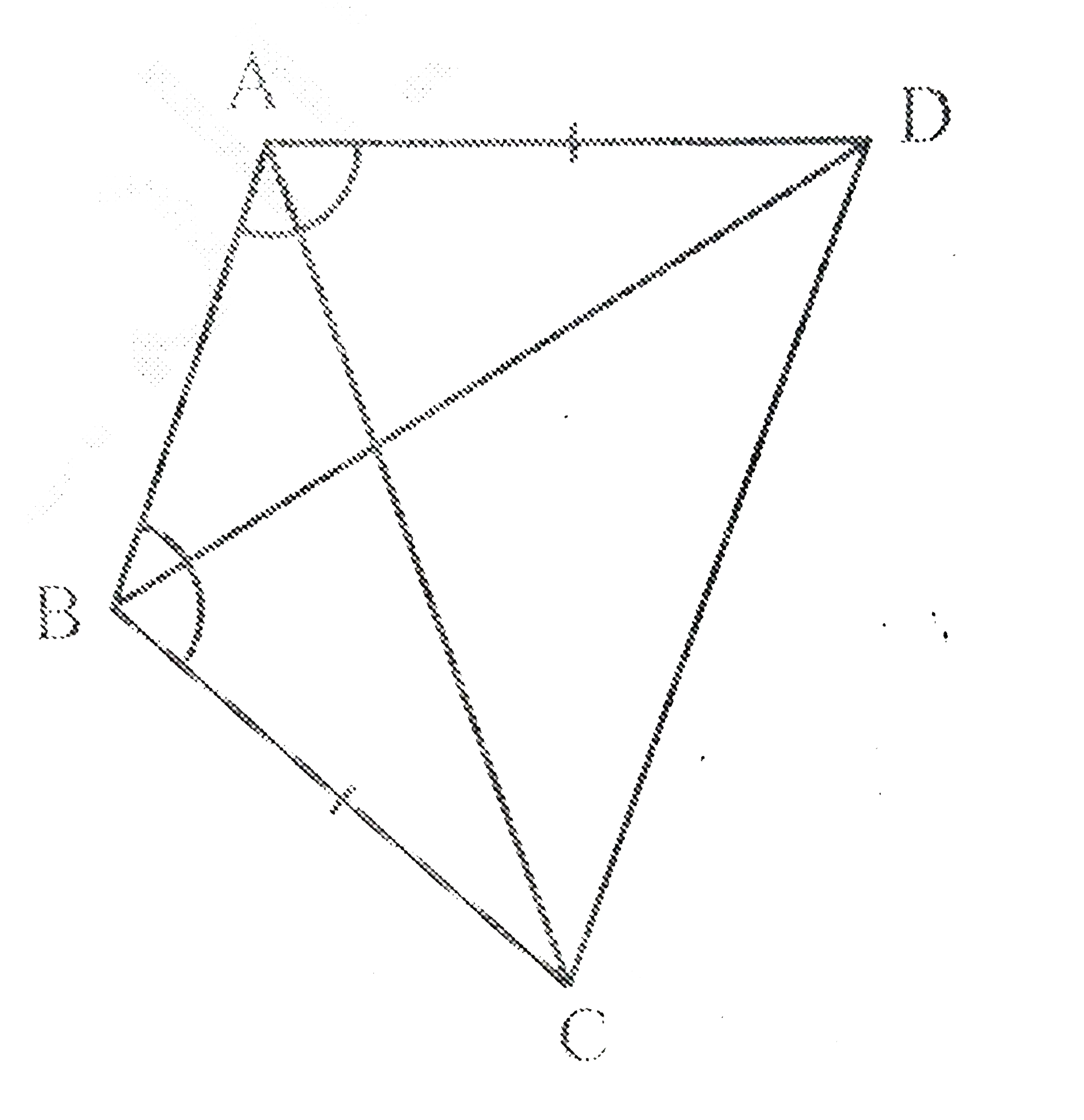
View SolutionABCD is a quadrilateral in which and∠DAB =∠CBA(see Fig. 7.17). Prove that
(i) ΔABD≅ΔBAC
(ii) BD = AC
(iii) ∠ABD =∠BAC
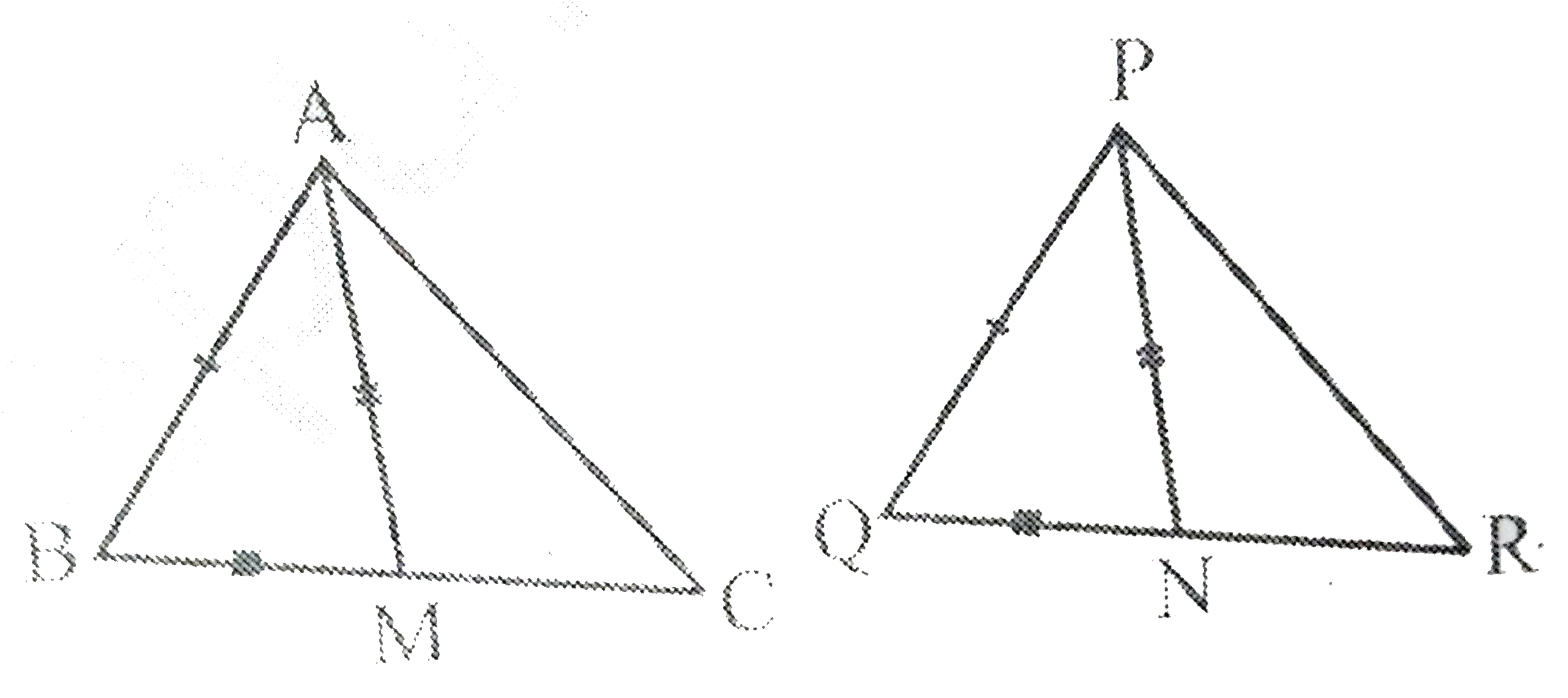
View SolutionTwo sides AB and BC and median AM of one triangle ABC are respectively equal to side PQ and QR and median PN of ΔPQR(see Fig. 7.40). Show that:
(i) ΔABM≅ΔPQN
(ii) ΔABC≅ΔPQR
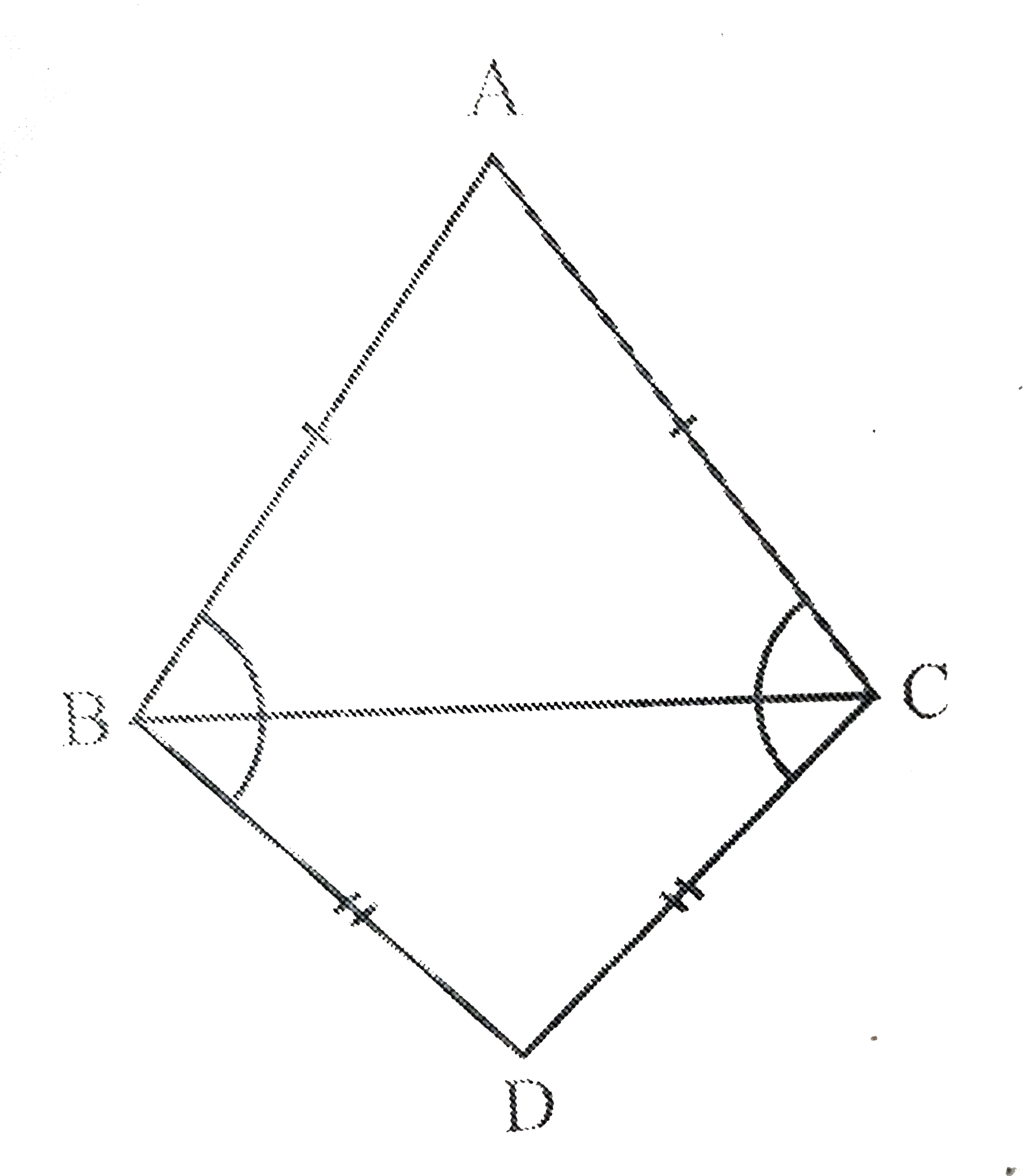
View SolutionABC and DBC are two isosceles triangles on the same base BC (see Fig. 7.33). Show that∠ABD =∠ACD
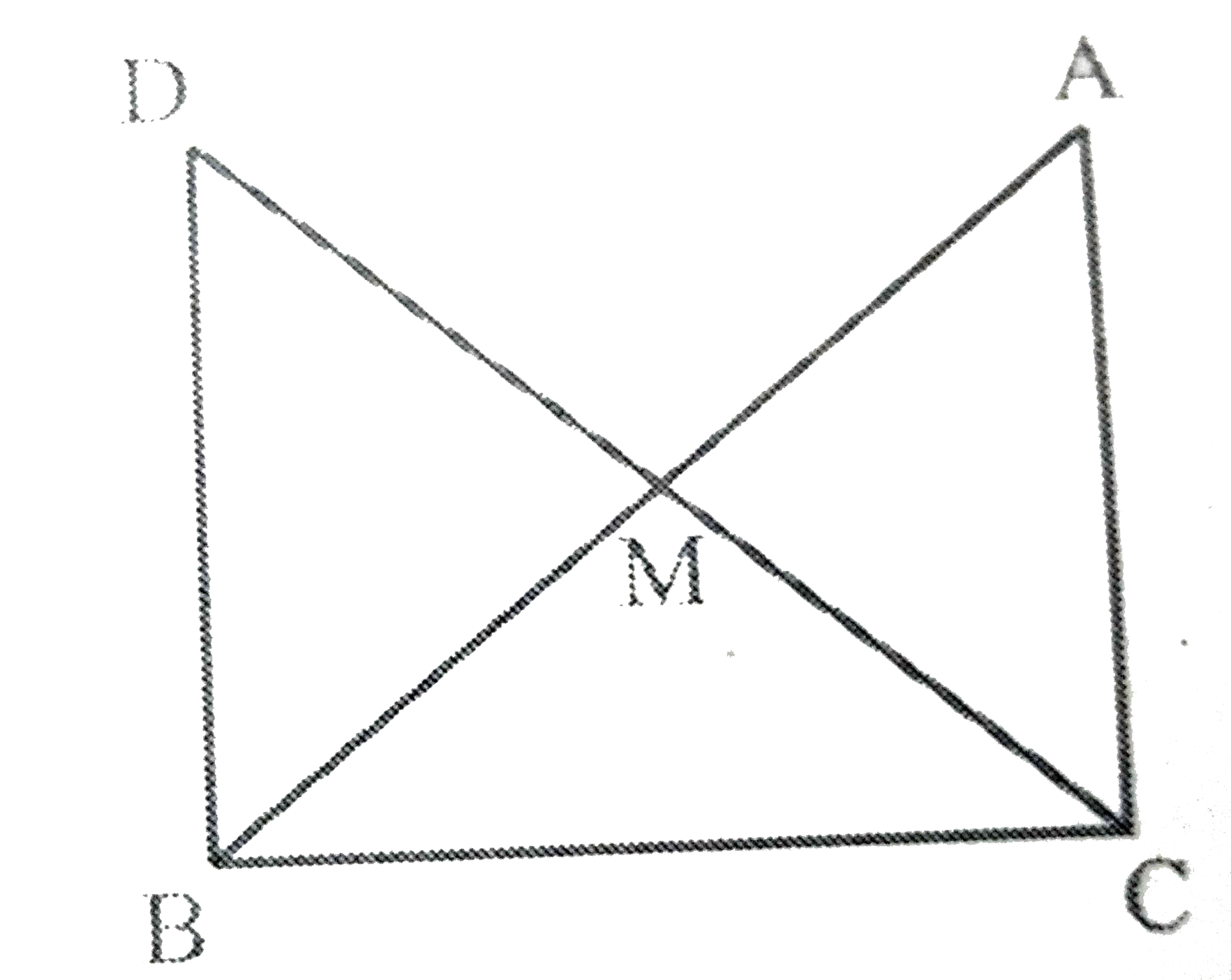
View SolutionIn figure, if ΔABE≅ΔACD, show that ΔADE~ΔABC.

View SolutionE and F are respectively the mid-points of equal sides AB and AC of ΔABC(see Fig. 7.28). Show that BF = C E.
View SolutionIn an isosceles triangle ABC with AB=AC, D and E are points on BCsuch that BE=CD(see Fig. 7.29). Show that AD=AE
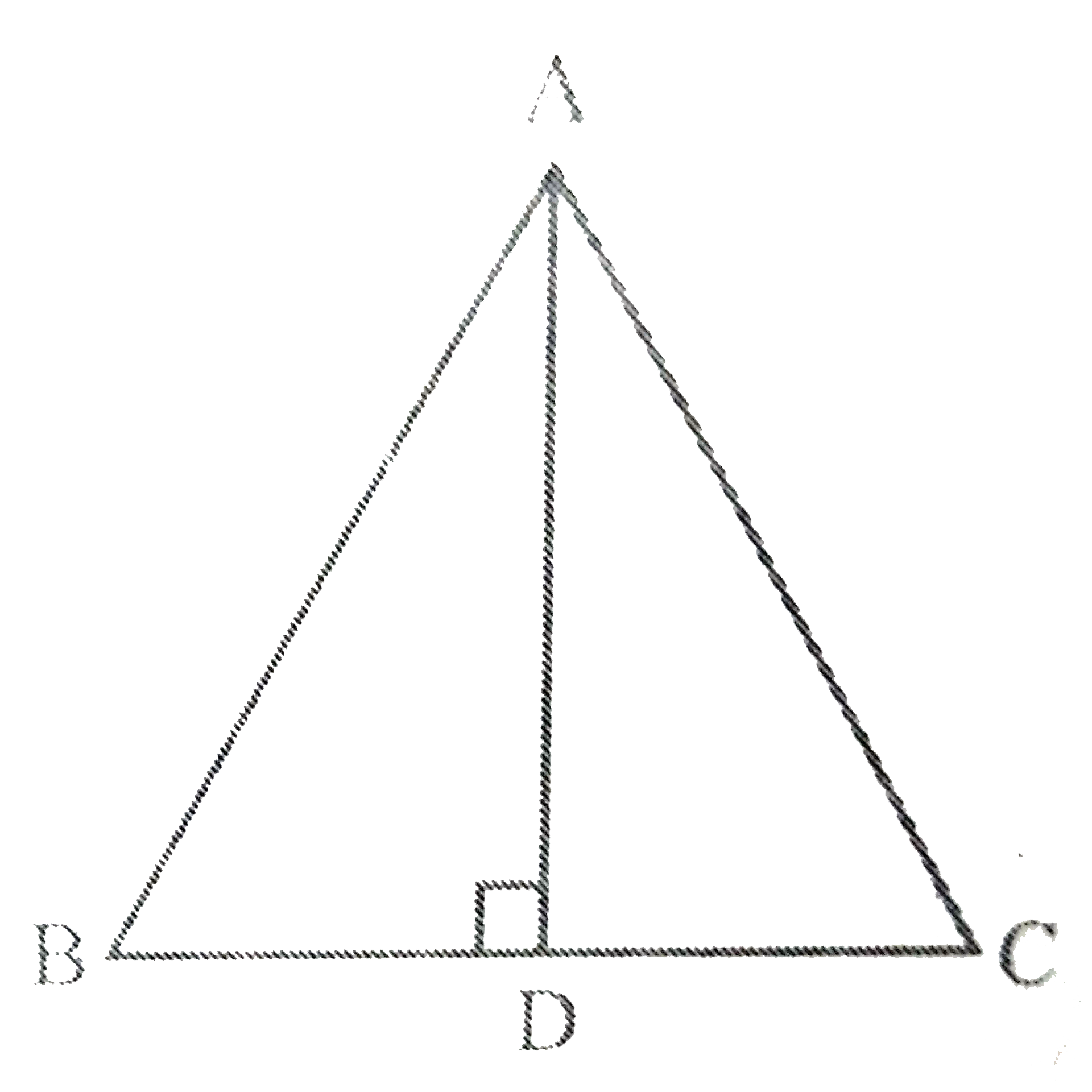
View SolutionIn ΔABC, AD is the perpendicular bisector of BC (see Fig. 7.30). Show that ΔABCis an isosceles triangle in which AB = AC.
View SolutionIn right triangle ABC, right-angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see Fig. 7.23). Show that:
(i) ΔAMC≅ΔBMD
(ii) ∠DBC is a right angle
(iii) ΔDBC≅ΔACB
(iv) CM=12AB
View Solution