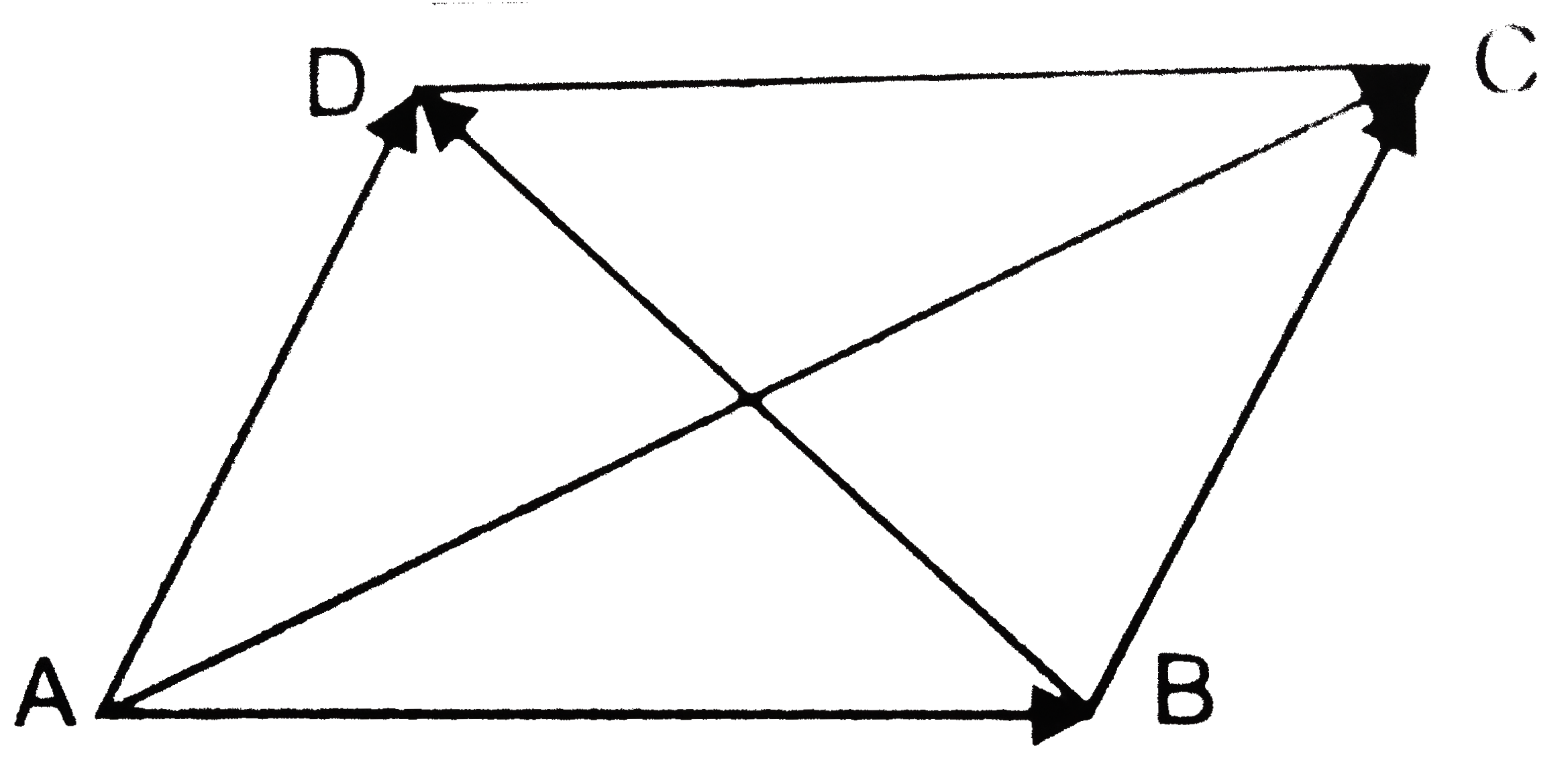
ABCD is a parallelogram and AC, BD are its diagonals. Show that :
$- - \to A C + - - \to B D = 2 - - \to B C, - - \to A C - - - \to B D = 2 - - \to A B$ .

Video Solution

Text Solution

Generated By DoubtnutGPT

To solve the problem, we need to show that for the parallelogram ABCD with diagonals AC and BD, the following two equations hold:
1. $\to A C + \to B D = 2 \to B C$
2. $\to A C - \to B D = 2 \to A B$
1. Define the Vectors:
- Let $\to A$ , $\to B$ , $\to C$ , and $\to D$ be the position vectors of points A, B, C, and D respectively.
- The vectors representing the sides of the parallelogram can be defined as:
- $\to A B = \to B - \to A$
- $\to B C = \to C - \to B$
- $\to C D = \to D - \to C$
- $\to D A = \to A - \to D$
2. Express the Diagonals:
- The diagonal $\to A C$ can be expressed as:
$\to A C = \to C - \to A$
- The diagonal $\to B D$ can be expressed as:
$\to B D = \to D - \to B$
3. Using the Properties of Parallelograms:
- In a parallelogram, opposite sides are equal and parallel. Thus, we have:
$\to A B = - \to C D and \to B C = - \to D A$
- This means:
$\to C D = \to B - \to A and \to D A = \to C - \to B$
4. Calculate $\to A C + \to B D$ :
- Substitute the expressions for $\to A C$ and $\to B D$ :
$\to A C + \to B D = (\to C - \to A) + (\to D - \to B)$
- Rearranging gives:
$= \to C + \to D - \to A - \to B$
- Since $\to D = \to C + \to B - \to A$ (from the properties of the parallelogram), we can substitute:
$= \to C + (\to C + \to B - \to A) - \to B - \to A$
- This simplifies to:
$= 2 \to B C$
5. Calculate $\to A C - \to B D$ :
- Now, we calculate $\to A C - \to B D$ :
$\to A C - \to B D = (\to C - \to A) - (\to D - \to B)$
- Rearranging gives:
$= \to C - \to A - \to D + \to B$
- Substitute $\to D = \to C + \to B - \to A$ :
$= \to C - \to A - (\to C + \to B - \to A) + \to B$
- This simplifies to:
$= 2 \to A B$
Conclusion
We have shown that:
1. $\to A C + \to B D = 2 \to B C$
2. $\to A C - \to B D = 2 \to A B$

Updated on:7/8/2024