ABCD is a parallelogram. P and Q are the mid-points of sides AB and AD reapectively.
Prove that area of triangle APQ= 18 of the area of parallelogram ABCD.
To prove that the area of triangle APQ is 18 of the area of parallelogram ABCD, we can follow these steps:
Step 1: Identify the Midpoints
Let P be the midpoint of side AB and Q be the midpoint of side AD.
Step 2: Draw the Diagonal
Draw the diagonal BD of the parallelogram ABCD. This diagonal divides the parallelogram into two triangles: △ABD and △BCD.
Step 3: Area of Triangle ABD
The area of triangle ABD is half of the area of the parallelogram ABCD. Therefore, we can write:
Area of △ABD=12×Area of ABCD
Step 4: Midpoint Theorem Application
Since P is the midpoint of AB and Q is the midpoint of AD, the line segment PQ will be parallel to BD and will divide triangle ABD into two smaller triangles of equal area. Thus, we can say:
Area of △APQ=12×Area of △ABD
Step 5: Substitute Area of Triangle ABD
Substituting the area of triangle ABD from Step 3 into the equation from Step 4:
Area of △APQ=12×(12×Area of ABCD)
This simplifies to:
Area of △APQ=14×Area of ABCD
Step 6: Area of Triangle BCD
Now, since PQ is also a mid-segment for triangle ABD, we can apply the same reasoning to triangle BCD. Thus, we can conclude:
Area of △APQ=14×Area of ABCD
Step 7: Final Calculation
Now, we need to find the area of triangle APQ in terms of the area of the parallelogram ABCD:
Area of △APQ=12×12×Area of ABCD=18×Area of ABCD
Conclusion
Thus, we have proved that:
Area of △APQ=18×Area of ABCD
Let P be the midpoint of side AB and Q be the midpoint of side AD.
Draw the diagonal BD of the parallelogram ABCD. This diagonal divides the parallelogram into two triangles: △ABD and △BCD.
The area of triangle ABD is half of the area of the parallelogram ABCD. Therefore, we can write:
Area of △ABD=12×Area of ABCD
Since P is the midpoint of AB and Q is the midpoint of AD, the line segment PQ will be parallel to BD and will divide triangle ABD into two smaller triangles of equal area. Thus, we can say:
Area of △APQ=12×Area of △ABD
Substituting the area of triangle ABD from Step 3 into the equation from Step 4:
Area of △APQ=12×(12×Area of ABCD)
This simplifies to:
Area of △APQ=14×Area of ABCD
Now, since PQ is also a mid-segment for triangle ABD, we can apply the same reasoning to triangle BCD. Thus, we can conclude:
Area of △APQ=14×Area of ABCD
Now, we need to find the area of triangle APQ in terms of the area of the parallelogram ABCD:
Area of △APQ=12×12×Area of ABCD=18×Area of ABCD
Thus, we have proved that:
Area of △APQ=18×Area of ABCD
Topper's Solved these Questions
- AREA THEOREMSBOOK - ICSECHAPTER - AREA THEOREMSEXERCISE - Exercies 16(C )
22 Videos
- AREA THEOREMSBOOK - ICSECHAPTER - AREA THEOREMSEXERCISE - Exercies 16(A)
36 Videos
- AREA AND PERIMETER OF PLANE FIGURESBOOK - ICSECHAPTER - AREA AND PERIMETER OF PLANE FIGURESEXERCISE - EXERCISE 20(D)
12 Videos
- CHAPTER REVISION (STAGE 2) BOOK - ICSECHAPTER - CHAPTER REVISION (STAGE 2) EXERCISE - DISTANCE FORMULA
12 Videos
Similar Questions
Knowledge Check

In the figure above, what is the area of parallelogram ABCD?A4√2B4√3C6√2D6√3
E, F, G and H are the mid-points of the sides of a parallelogram ABCD. Show that area of quadrilateral EFGH is half of the area of parallelogram ABCD.
View SolutionABCD is a parallelogram E is mid-point of AB and DE bisects angle D. Prove that

∠DEC=90∘
View SolutionABCD is a parallelogram E is mid-point of AB and DE bisects angle D. Prove that
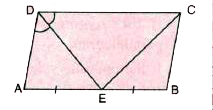
CE bisects angle C
View SolutionABCD is a parallelogram. Two points P and Q are taken on sides AD and BC respectively such that AP 13ADandCQ=13BC. Prove that □AQCP is a parallelogram.
View SolutionD, E and F are the mid-points of the sides BC, CA and AB respectively of triangle ABC. Prove that:
BDEF is a parallelogram.
View SolutionIn parallelogram ABCD, X and Y are mid-points of opposite sides AB and DC respectively. Prove that:
(i) AX=YC.
(ii) AX is parallel to YC
(iii) AXCY is a parallelogram.
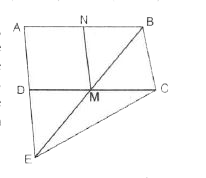
View SolutionIn the given figure, M and N are the mid-points of the sides DC and AB respectively of the parallelogram ABCD.
If the area of parallelogram ABCD is 48cm2,
(i) State the area of the triangle BEC.
(ii) name the parallelofram which is equal in area to the triangle BEC.
View Solution

