ABCD is a rectangle with A(−1,2),B(3,7) and AB:BC=4:3. If P is the centre of the rectangle, then the distance of P from each corner is equal to
√142
3√414
2√413
5√418
The correct Answer is:D
Since ABCD is a rectangle, (AC)2=(AB)2+(BC)2
=(AB)2[1+916]=2516(AB)2
and PA=AC2=5AB8
58√(−1−3)2+(2−7)2=5√418
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSYEM EXERCISE - Multiple correct13videos
COORDINATE SYSYEM
- BOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSYEM EXERCISE - Linked10videos
COORDINATE SYSYEM
- BOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSYEM EXERCISE - Concept applications 1.69videos
COORDINATE SYSYEM
- BOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type2videos
COORDINATE SYSTEM
- BOOK - CENGAGE ENGLISHCHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.213videos
CROSS PRODUCTS
Similar Questions
ABCD is a rectangle with A(-1,2) , B (3,7) and AB : BC = 4 : 3 . If d is the distance from the vertices of the rectangle then [d] is equal to (where [.] denotes the greatest integer function ).
View SolutionIn a rectangle ABCD,AB=2l and BC=l. Axes × and yy pass through centre of the rectangle. The moment of inertia is least about :
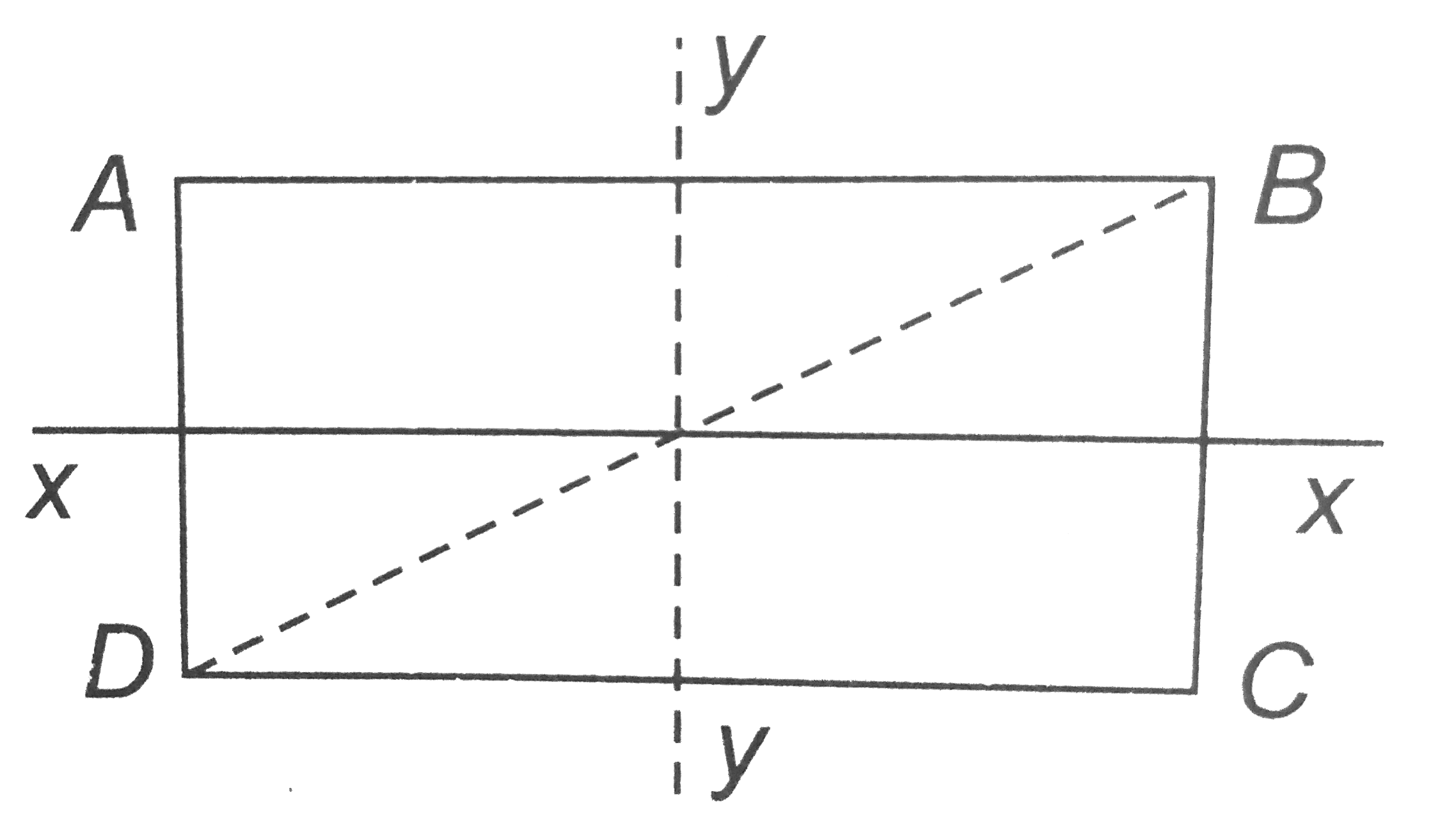 .View Solution
.View Solution
Knowledge Check
- Question 1 - Select One
In the figure, ABCD is a rectangle. Points E and F cut the sides BC and CD of the rectangle respectively such that EC = 3, FC = 4, and AD = 12, and the area of the crossed and the shaded regions in the figure are equal. Which one of the following equals the perimeter of rectangle ABCD?
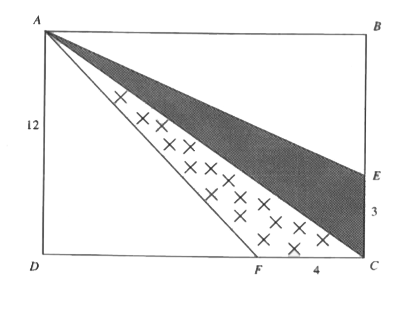 A42B50C56D64
A42B50C56D64
The points A (-1,-2), B (4,3) ,C (2,5) and D (-3,0) in that order form a rectangle.
View SolutionABCD is a rectangle wih sides AB=p, BC=q,. If AB and AD are taken negative directions of coordinate axes. then the equaton of the circumscribing the rectangle is
View SolutionPoints A (1, 3) and C (5, 1) are opposite vertices of a rectangle ABCD. If the slope of BD is 2, then its equation is
View SolutionA(1, 3) and C(5, 1) are two opposite vertices of a rectangle ABCD. If the slope of BD is 2, then the coordinates of B can be :
View SolutionA circle passing through the vertex C of a rectangle ABCD and touching its sides AB and AD at M and N, respectively. If the distance from C to the line segment MN is equal to 5 units, then find the area of the reactangle ABCD.
View SolutionIn the figure given below, ABCD is a rectangle. AB = 14 cm, BC = 7 cm. From the rectangle, a quarter circle BFEC and a semicircle DGE are removed. Calculate the area of the remaining piece of the rectangle. (Take π=227)
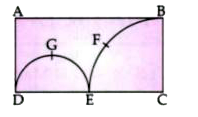 View Solution
View SolutionP1,P2,P3 are altitudes of a triangle ABC from the vertices A, B, C and Δ is the area of the triangle,
The value of P−11+P−12+P−13 is equal to-View Solution

