ABCD is a rectangle wih sides AB=p, BC=q,. If AB and AD are taken negative directions of coordinate axes. then the equaton of the circumscribing the rectangle is
a) x2+y2+px+qy=0
b) x2+y2−px−qy=0
c) x2+y2+2px+2qy=0
d) x2+y2−2px−2qy=0
The correct Answer is:A
To find the equation of the circle circumscribing the rectangle ABCD with sides AB = p and BC = q, where AB and AD are taken in the negative directions of the coordinate axes, we can follow these steps:
Step 1: Define the coordinates of the rectangle
Given that AB = p and BC = q, we can place the rectangle in the coordinate system as follows:
- Point A (0, 0) (the origin)
- Point B (-p, 0) (moving p units left on the x-axis)
- Point C (-p, -q) (moving q units down on the y-axis)
- Point D (0, -q) (moving back to the y-axis)
Step 2: Identify the center of the circumscribing circle
The center of the circumscribing circle of a rectangle is at the midpoint of the diagonal connecting opposite corners. We can find the midpoint of AC (or BD) as follows:
- Midpoint M = (xA+xC2,yA+yC2)
- Substituting the coordinates of A and C:
M=(0+(−p)2,0+(−q)2)=(−p2,−q2)
Step 3: Calculate the radius of the circumscribing circle
The radius R of the circle can be found using the distance formula from the center to any vertex of the rectangle (let's use point A):
R=√(−p2−0)2+(−q2−0)2=√(−p2)2+(−q2)2
=√p24+q24=12√p2+q2
Step 4: Write the equation of the circle
The general equation of a circle with center (h, k) and radius r is given by:
(x−h)2+(y−k)2=r2
Substituting the center M and radius R:
(x+p2)2+(y+q2)2=(12√p2+q2)2
(x+p2)2+(y+q2)2=p2+q24
Step 5: Expand the equation
Expanding the left side:
(x2+px+p24)+(y2+qy+q24)=p2+q24
Combining terms:
x2+y2+px+qy+p2+q24−p2+q24=0
Thus, we have:
x2+y2+px+qy=0
Final Answer
The equation of the circle circumscribing the rectangle ABCD is:
x2+y2+px+qy=0
Given that AB = p and BC = q, we can place the rectangle in the coordinate system as follows:
- Point A (0, 0) (the origin)
- Point B (-p, 0) (moving p units left on the x-axis)
- Point C (-p, -q) (moving q units down on the y-axis)
- Point D (0, -q) (moving back to the y-axis)
The center of the circumscribing circle of a rectangle is at the midpoint of the diagonal connecting opposite corners. We can find the midpoint of AC (or BD) as follows:
- Midpoint M = (xA+xC2,yA+yC2)
- Substituting the coordinates of A and C:
M=(0+(−p)2,0+(−q)2)=(−p2,−q2)
The radius R of the circle can be found using the distance formula from the center to any vertex of the rectangle (let's use point A):
R=√(−p2−0)2+(−q2−0)2=√(−p2)2+(−q2)2
=√p24+q24=12√p2+q2
The general equation of a circle with center (h, k) and radius r is given by:
(x−h)2+(y−k)2=r2
Substituting the center M and radius R:
(x+p2)2+(y+q2)2=(12√p2+q2)2
(x+p2)2+(y+q2)2=p2+q24
Expanding the left side:
(x2+px+p24)+(y2+qy+q24)=p2+q24
Combining terms:
x2+y2+px+qy+p2+q24−p2+q24=0
Thus, we have:
x2+y2+px+qy=0
The equation of the circle circumscribing the rectangle ABCD is:
x2+y2+px+qy=0
Similar Questions
ABCD is a square with side a. If AB and AD are taken as positive coordinate axes then equation of circle circumscribing the square is
View SolutionABCD is a square in first quadrant whose side is a, taking ABandAD as axes, prove that the equation to the circle circumscribing the square is x2+y2=a(x+y).
View Solution
Knowledge Check
In the figure, ABCD is a rectangle and E is a point on the side AB. If AB=10andAD=5 what is the area of the shaded region in the figure?
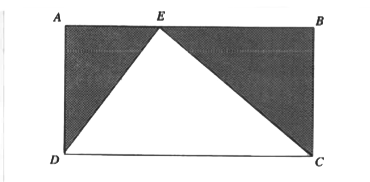 A25B30C35D40
A25B30C35D40
ABCD is a rectangle with A(−1,2),B(3,7) and AB:BC=4:3. If P is the centre of the rectangle, then the distance of P from each corner is equal to
View SolutionABCD is a rectangle with A(-1,2) , B (3,7) and AB : BC = 4 : 3 . If d is the distance from the vertices of the rectangle then [d] is equal to (where [.] denotes the greatest integer function ).
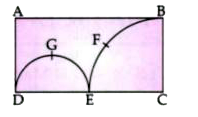
View SolutionIn the figure given below, ABCD is a rectangle. AB = 14 cm, BC = 7 cm. From the rectangle, a quarter circle BFEC and a semicircle DGE are removed. Calculate the area of the remaining piece of the rectangle. (Take π=227)
View SolutionIf AB is the intercept of the tangent to the circle x2+y2=r2 between the coordinate axes, the locus of the vertex P of the rectangle OAPB is
View SolutionABCD is a rectangle. A circle passing through vertex C touches the sides AB and AD at M and N respectively. If the distance lof the line MN from the vertex C is P units then the area of rectangle ABCD is
View SolutionLet ABCD be a rectangle such that AB=10 units and BC=8 units. Taking AB and AD as x and y axis respectively, find the coordinates of A, B, C and D.
View SolutionParallelogram ABCD and rectangle ABEF are on the same base AB and have equal areas. Show that the perimeter of the parallelogram is greater than that of the rectangle.
View Solution
