ABCD is a rhombus. RABS is a straight line such that RA = AB = BS. Prove that RD and SC when produced meet at right angles.
Step by step video, text & image solution for ABCD is a rhombus. RABS is a straight line such that RA = AB = BS. Prove that RD and SC when produced meet at right angles. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- QUADRILATERALSBOOK - NAGEEN PRAKASHANCHAPTER - QUADRILATERALSEXERCISE - Revision Exercise (short Answer Questions )
10 Videos
- PROBABILITYBOOK - NAGEEN PRAKASHANCHAPTER - PROBABILITYEXERCISE - Revision Exercise (very Short Answer /short Answer Questions)
10 Videos
- STATISTICSBOOK - NAGEEN PRAKASHANCHAPTER - STATISTICSEXERCISE - Revision Exercise
10 Videos
Similar Questions
ABCD is a rhombus, EABF is a straight line such that EA=AB=BF . Prove that ED and FC when produced meet at right angles.
View SolutionABCD is a parallelogram. Side AB is produced on both sides to E & F as in figure such that BE = BC & AF = AD. Show that EC & FD when produced meets at right angle.
View Solution
Knowledge Check
ABCD is a rhombus, AB is extended to F and BA to E such that AB = AE = BF then what is the result?
AED>CFBEDI_CFCED2+CF2=EF2DED∣∣CFABCD is a rhombus, AB is extended to F and BA to E such that AB = AE = BF then what is the result?
AED2+CF2=EF2BED/CFCED>CFDED1CFABCD is a rhombus. A line passing through C cuts extended line AD and AB at Q and P respectively. If QD=12AB. Then find the ratio AB to PB.
 A2:1B1:2C1:1D3:1
A2:1B1:2C1:1D3:1
ABCD is a parallelogram. AB is produced to E so that BE=AB . Prove that ED bisects BC.
View SolutionABCD is a parallelogram and APQ is a straight line meeting BC at PandDC produced at Q. prove that the rectangle obtained by BPandDQ is equal to the rectangle contained by ABandBC.
View SolutionABCD is a parallelogram and APQ is a straight line meeting BC at Pand DC produced at Q. prove that the rectangle obtained by BP and DQ is equal to the rectangle contained by AB and BC.
View SolutionABCD is a rhombus, AB is extended to F and BA to E such that AB = AE = BF then what is the result?
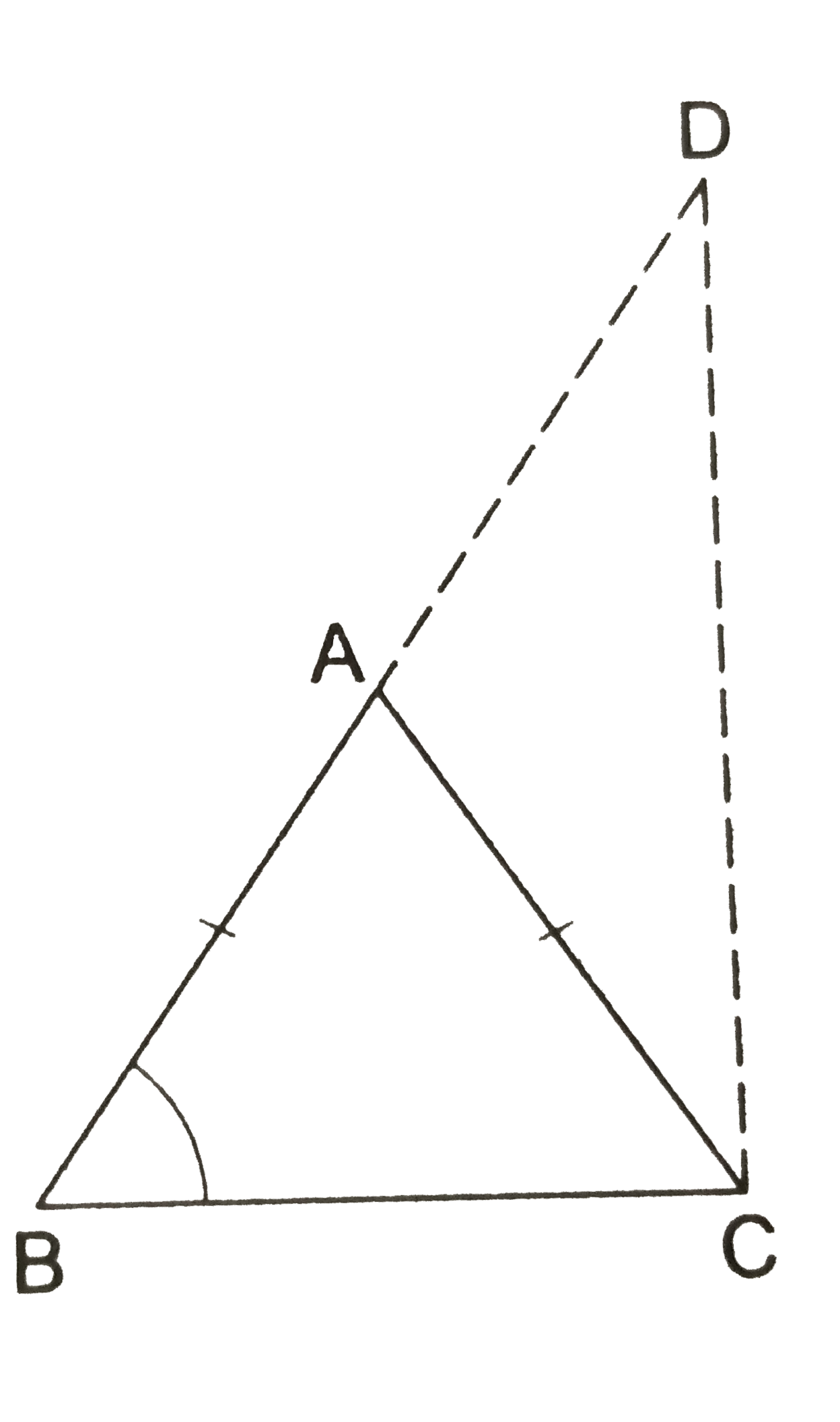
View SolutionΔABC is an isosceles triangle with AB = AC.
Side BA is produced to D such that AB = AD.
Prove that ∠BCD is a right angle.
View Solution
