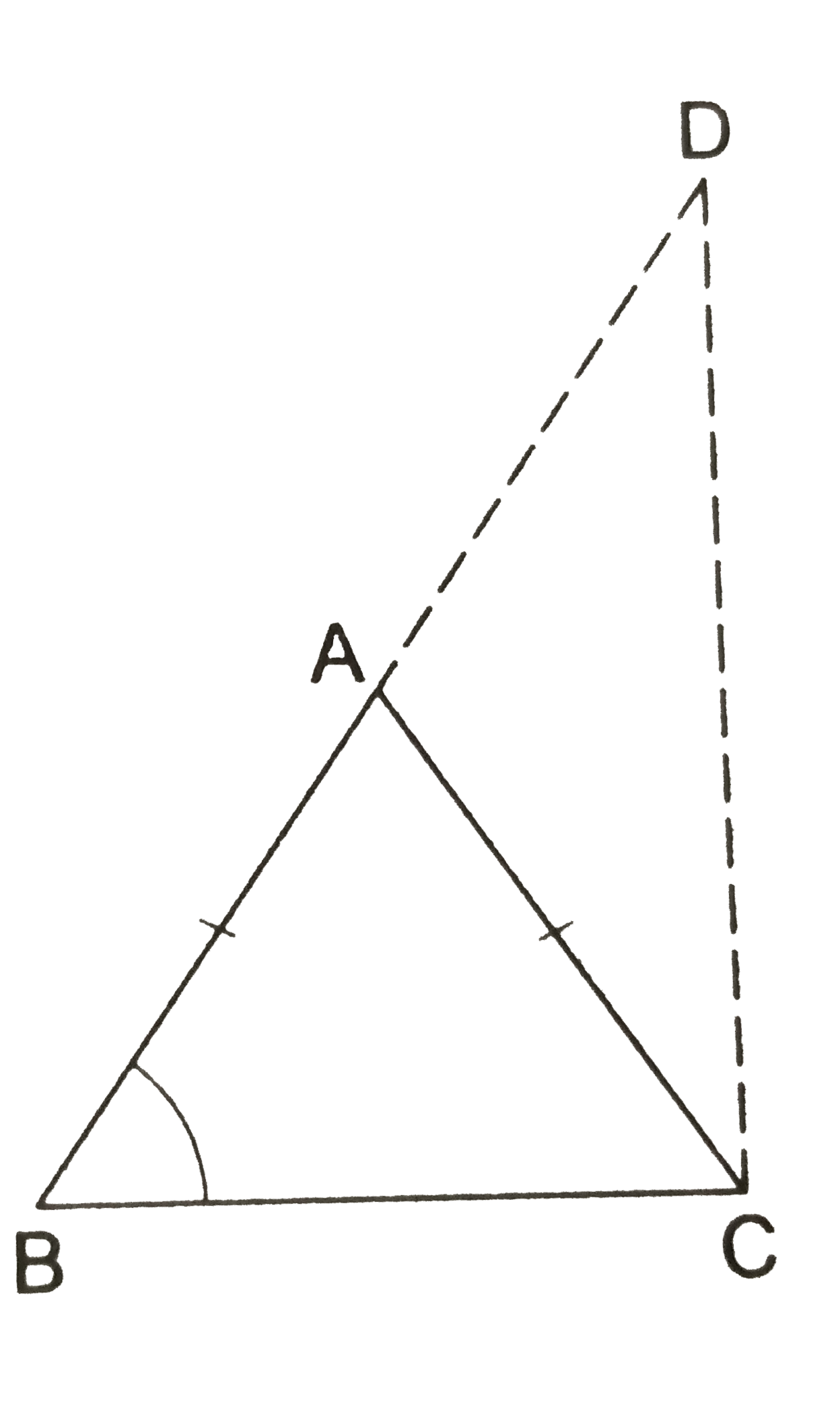
$Δ A B C$ is an isosceles triangle with AB = AC.
Side BA is produced to D such that AB = AD.
Prove that $∠ B C D$ is a right angle.

Video Solution

Text Solution

Verified by Experts

GIVEN A $Δ A B C in which A B = A C$ and BA is produced to D such that AB = AD.
TO PROVE $∠ B C D = 90^{\circ}$
CONSTRUCTIONS Produced BA to D such that BA = AD.
Join DC.
PROOF $A B = A C and A B = A D \Rightarrow A D = A C$ .
Now, $A B = A C \Rightarrow ∠ A B C = ∠ A C B,$
$A D = A C \Rightarrow ∠ A D C = ∠ A C D$ .
$∴ ∠ A B C + ∠ A D C = ∠ A C B + ∠ A C D$
$\Rightarrow ∠ A B C + ∠ A D C = ∠ B C D [∵ ∠ A C B + ∠ A C D = ∠ B C D]$
$\Rightarrow ∠ A B C + ∠ A D C + ∠ B C D = 2 ∠ B C D$
$[adding ∠ B C D on both sides]$
$\Rightarrow 2 ∠ B C D = 180^{\circ} [∵ sum of the ∠ s of Δ A B D is 180^{\circ}]$
$\Rightarrow ∠ B C D = 90^{\circ}$ .
Hence, $∠ B C D$ is a right angle.

Updated on:21/07/2023