ABCD is a trapezium such that AB∣∣CDandCB is perpendicular to them. If ∠ADB=θ,BC=p,andCD=q , show that AB=(p2+q2)sinθpcosθ+qsinθ
Let ∠ABD=∠BDC=α
∴Ang≤BAD=180∘−(θ+α)
By the sine formula, in ΔABD, we have
ABsinθ=BDsin(180∘−(θ+α))
or AB=BDsinθsin(θ+α)=BDsinθsinθcosα+cosθsinα (i)

In ΔBCD,sinα=p/BD
and cosα=q/BD
Also BD2=p2+q2
Therefore, from Eq. (i), we have
AB=BDsinθsinθ(q/BD)+cosθ(p/BD)
=BD2sinθqsinθ+pcosθ=(p2+q2)sinθpcosθ+qsinθ
Topper's Solved these Questions
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGECHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Exercise 5.1
12 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGECHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Exercise 5.2
8 Videos
- PROGRESSION AND SERIESBOOK - CENGAGECHAPTER - PROGRESSION AND SERIESEXERCISE - ARCHIVES (MATRIX MATCH TYPE )
1 Videos
- PROPERTIES OF TRIANGLE, HEIGHT AND DISTANCEBOOK - CENGAGECHAPTER - PROPERTIES OF TRIANGLE, HEIGHT AND DISTANCEEXERCISE - Question Bank
32 Videos
Similar Questions
ABCD is a trapezium such that AB∣∣CDandCB is perpendicular to them. If ∠ADB=θ,BC=p,andCD=q , show that AB=(p2+q2)sinθpcosθ+qsinθ
View SolutionABCD is a trapezium such that AB and CD are parallel and BC⊥CD . If ∠ADB=θ,BC=pandCD=q , then AB is equal to (1) p2+q2cosθpcosθ+qsinθ (2) p2+q2p2cosθ+q2sinθ (3) (p2+q2)sinθ(pcosθ+qsinθ)2 (4) (p2+q2)sinθpcosθ+qsinθ
View SolutionABCD is a trapezium in which AB∣∣DC and ∠A=∠B=40∘. Find ∠C and ∠D. Are these angles equal?
View SolutionABCD is a trapezium in which AB∣∣DC ∠A=∠B=30degree. Find ∠C and ∠D. Are these angles equal?

View SolutionABCD is a trapezium in which ABDC . P and Q are points on sides AD and BC such that PQAB . If PD=18 , BQ=35 and QC=15 , find AD .
View SolutionIf psinθ+qcosθ=3&qsinθ−pcosθ=2, then p2+q2=?
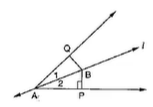
View SolutionIn Figure, line l is the bisector of angle A and B is any point on l.BP and BQ are perpendiculars from B to the arms of A. Show that: APB ≅AQB BP=BQ or B is equidistant from the arms of ∠A
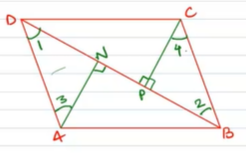
View SolutionIn Figure, AN and CP are perpendicular to the diagonal BD of a parallelogram ABCD. Prove that : ADN≅CBP (ii) AN=CP
View SolutionABCD is a cyclic quadrilateral whose diagonals ACandBD intersect at P . If AB=DC, Prove that : PAB≅PDC PA=PDandPC=PB ADBC
View Solutionline l is the bisector of an angle ∠A and∠Bis any point on l. BP and BQ are perpendiculars from B to the arms of ∠A. Show that:
(i) ΔAPB≅ΔAQB
(ii) BP = BQ or B is equidistant from the arms of ∠A

View Solution
