ABCDE is a regular pentagon. The bisector of angle A of the pentagon meet the side CD in point M. Show that ∠AMC=90∘. 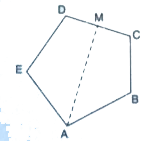
Step by step video & image solution for ABCDE is a regular pentagon. The bisector of angle A of the pentagon meet the side CD in point M. Show that angleAMC=90^@. by Maths experts to help you in doubts & scoring excellent marks in Class 8 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
ABCDE is a regular pentagon. The bisector of ∠A of the pentagon meets the side CD in M. Show that ∠AMC=900.
View SolutionIn triangle ABC, side AC is greater than side AB. If the internal bisector of angle A meets the opposite side at point D, prove that : ∠ADC is greater than ∠ADB.
View SolutionIn triangle ABC, side AC is greater than side AB. If the internal bisector of angle A meets the opposite side at point D, prove that : ∠ADC is greater than ∠ADB.
View SolutionIn ΔABC, angle ABC is equal to twice the angle ACB, and bisector of angle ABC meets the opposite side at point P. Show that :
AB×BC=BP×CA
View SolutionIn a parallelogram ABCD, the bisectors of ∠Aand∠B intersect each other at point P. Prove that ∠APB=90∘.
View SolutionIn ΔABC, angle ABC is equal to twice the angle ACB, and bisector of angle ABC meets the opposite side at point P. Show that :
CB:BA=CP:PA
View SolutionIn a parallelogram ABCD, ∠BCD=60∘ If the bisectors AP and BP of ∠Aand∠B respectively, meet the side CD at point P, then prove that CP = PD.
View SolutionIn parallelogram ABCD, the bisectors of adjacent angles A and D intersect each other at point P. prove that ∠APD=90∘.
View SolutionBisectors of angles A and B of a parallelogram ABCD meet at point M. Prove that ∠AMB=12(∠C+∠D)
View SolutionIn triangle ABC,the bisector of interior angle A and the bisector angle C meet at point O. Prove that ∠AOC=12∠B
View Solution