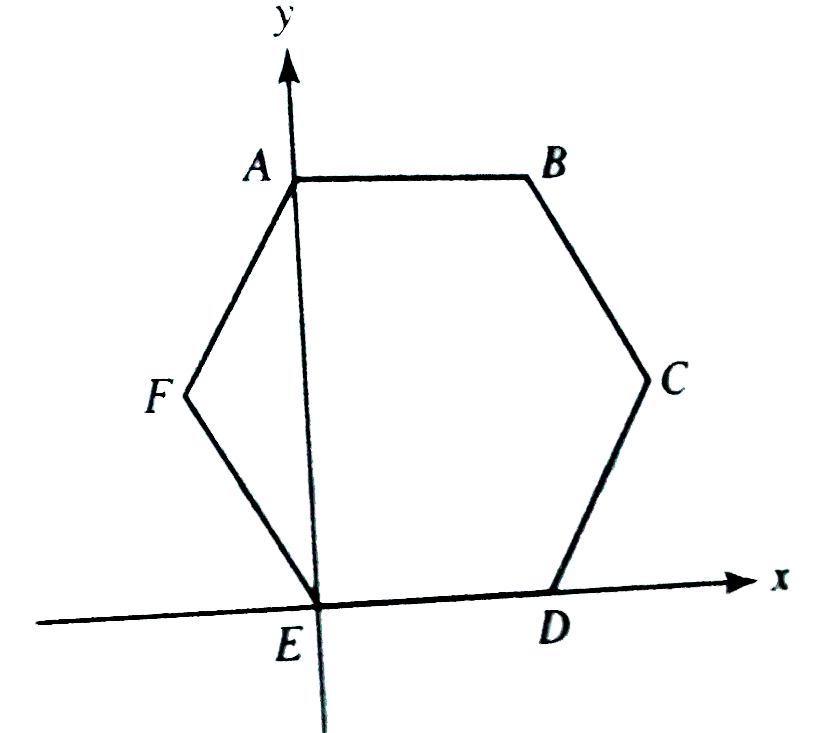
ABCDEF is a regular hexagon in the x-y plance with vertices in the anticlockwise direction. If →AB=2ˆi, then →CD is
ˆi+√3ˆj
ˆi−√3ˆj
−ˆi+√3ˆj
√3ˆi−ˆj
The correct Answer is:C
To find the vector →CD in the regular hexagon ABCDEF where →AB=2^i, we can follow these steps:
Step 1: Understand the Geometry of the Hexagon
A regular hexagon can be divided into 6 equilateral triangles. The internal angles of a regular hexagon are 120∘. The vertices A,B,C,D,E,F can be represented in the Cartesian plane.
Step 2: Place the Hexagon in the Coordinate System
Let's place vertex A at the origin (0,0) and vertex B at (2,0) since →AB=2^i.
Step 3: Determine the Coordinates of Other Vertices
Using the properties of the hexagon:
- The coordinates of C can be found by rotating B by 60∘ counterclockwise around A:
C=(2cos(60∘),2sin(60∘))=(2⋅12,2⋅√32)=(1,√3)
- The coordinates of D can be found by rotating C by 60∘ counterclockwise:
D=(2cos(120∘),2sin(120∘))=(2⋅−12,2⋅√32)=(−1,√3)
Step 4: Calculate the Vector →CD
The vector →CD can be calculated as:
→CD=→D−→C=(−1,√3)−(1,√3)=(−1−1,√3−√3)=(−2,0)
Step 5: Write the Result in Vector Notation
Thus, the vector →CD is:
→CD=−2^i
Conclusion
The final answer is:
→CD=−2^i
---
A regular hexagon can be divided into 6 equilateral triangles. The internal angles of a regular hexagon are 120∘. The vertices A,B,C,D,E,F can be represented in the Cartesian plane.
Let's place vertex A at the origin (0,0) and vertex B at (2,0) since →AB=2^i.
Using the properties of the hexagon:
- The coordinates of C can be found by rotating B by 60∘ counterclockwise around A:
C=(2cos(60∘),2sin(60∘))=(2⋅12,2⋅√32)=(1,√3)
D=(2cos(120∘),2sin(120∘))=(2⋅−12,2⋅√32)=(−1,√3)
The vector →CD can be calculated as:
→CD=→D−→C=(−1,√3)−(1,√3)=(−1−1,√3−√3)=(−2,0)
Thus, the vector →CD is:
→CD=−2^i
The final answer is:
→CD=−2^i
Topper's Solved these Questions
Similar Questions
Knowledge Check
ABCDEF is a regular hexagon . What is the slope of the line containing ¯¯¯¯¯¯FE ?A−12B−√3C−√2D√3
Consider the regular hexagon ABCDEF with centre at O (origin).
Q. AD+EB+FC is equal to
View SolutionIf ABCDEF is a regular hexagon then −−→AD+−−→EB+−−→FC equals :
View SolutionIn a regular hexagon ABCDEF, −−→AE
View SolutionIf ABCDEF is a regular hexagon with −−→AB=→a and −−→BC=→b, then −−→CE equals
View SolutionFigure below show regular hexagons with charges at the vertices. In which of the following cases the electric field at the centre is not zero
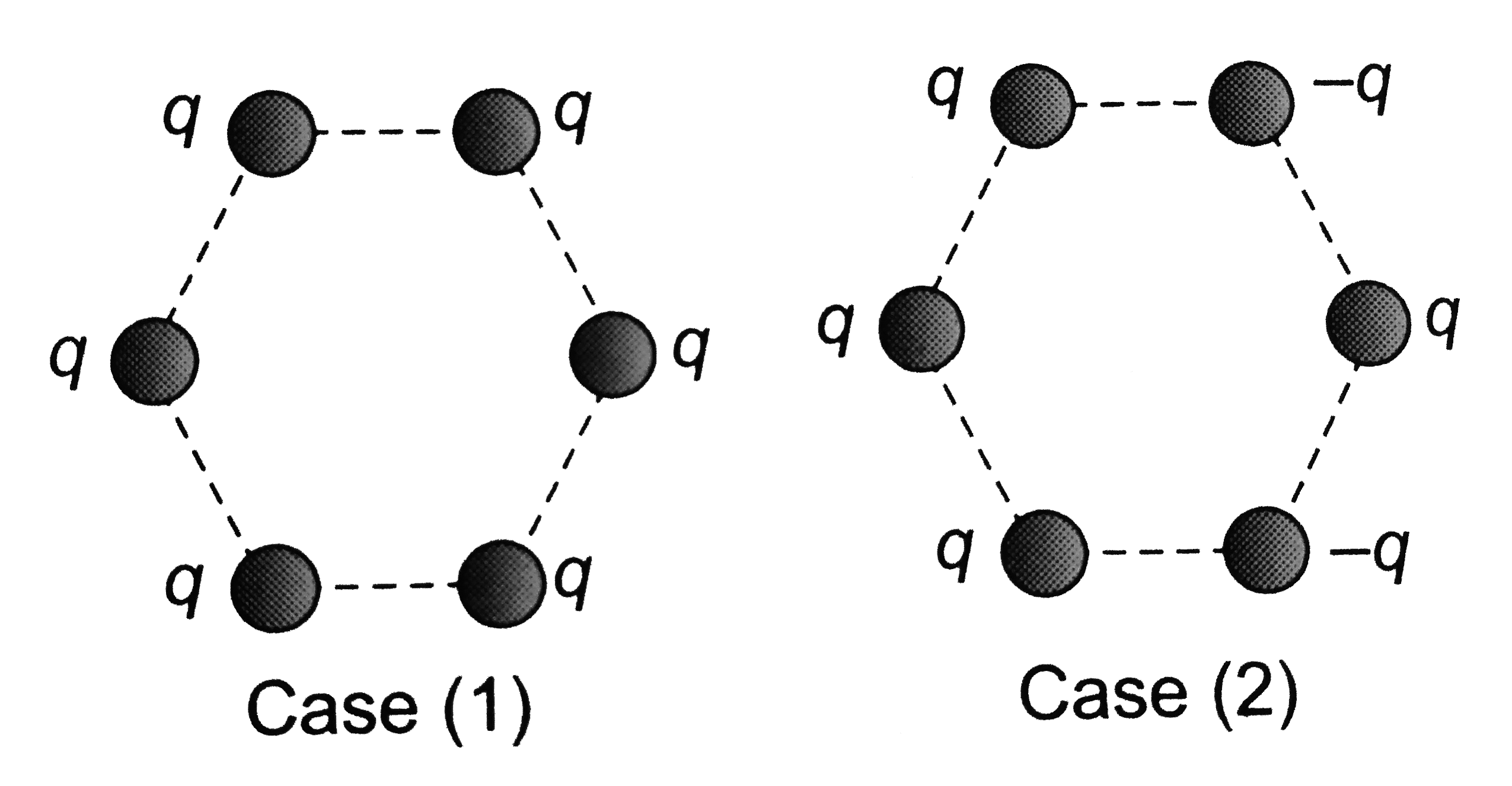
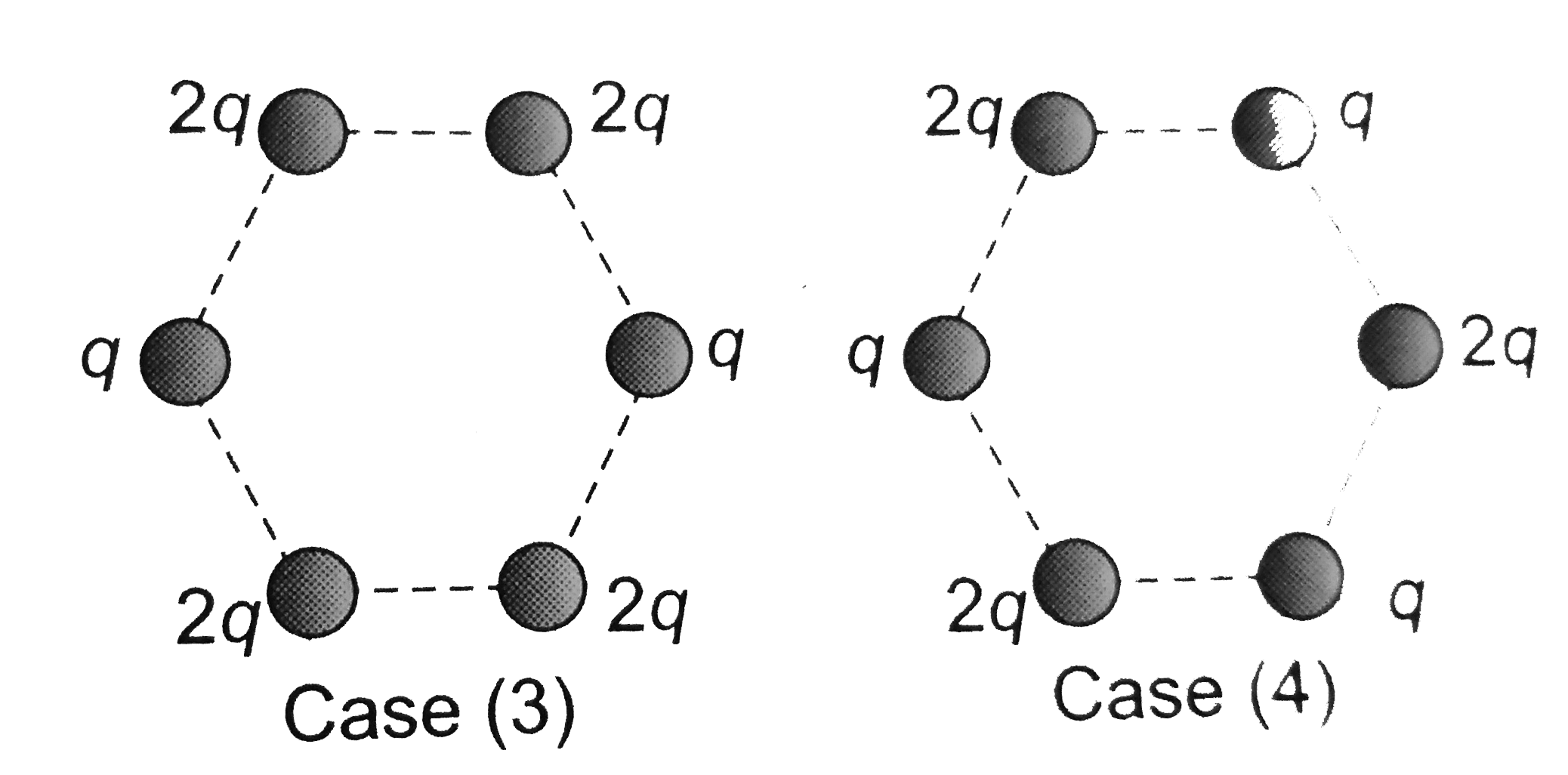
View SolutionIf center of a regular hexagon is at the origin and one of the vertices on the Argand diagram is 1+2i , then its perimeter is 2√5 b. 6√2 c. 4√5 d. 6√5
View SolutionOABCDE is a regular hexagon of side 2 units in the XY-plane in the first quadrant. O being the origin and OA taken along the x-axis. A point P is taken on a line parallel to the z-axis through the centre of the hexagon at a distance of 3 unit from O in the positive Z direction. Then find vector AP.
View Solution
