ABCP is a quadrant of a circle of radius 14 cm. with AC as diameter, a semicircle is drawn. Find the area of the shaded portion
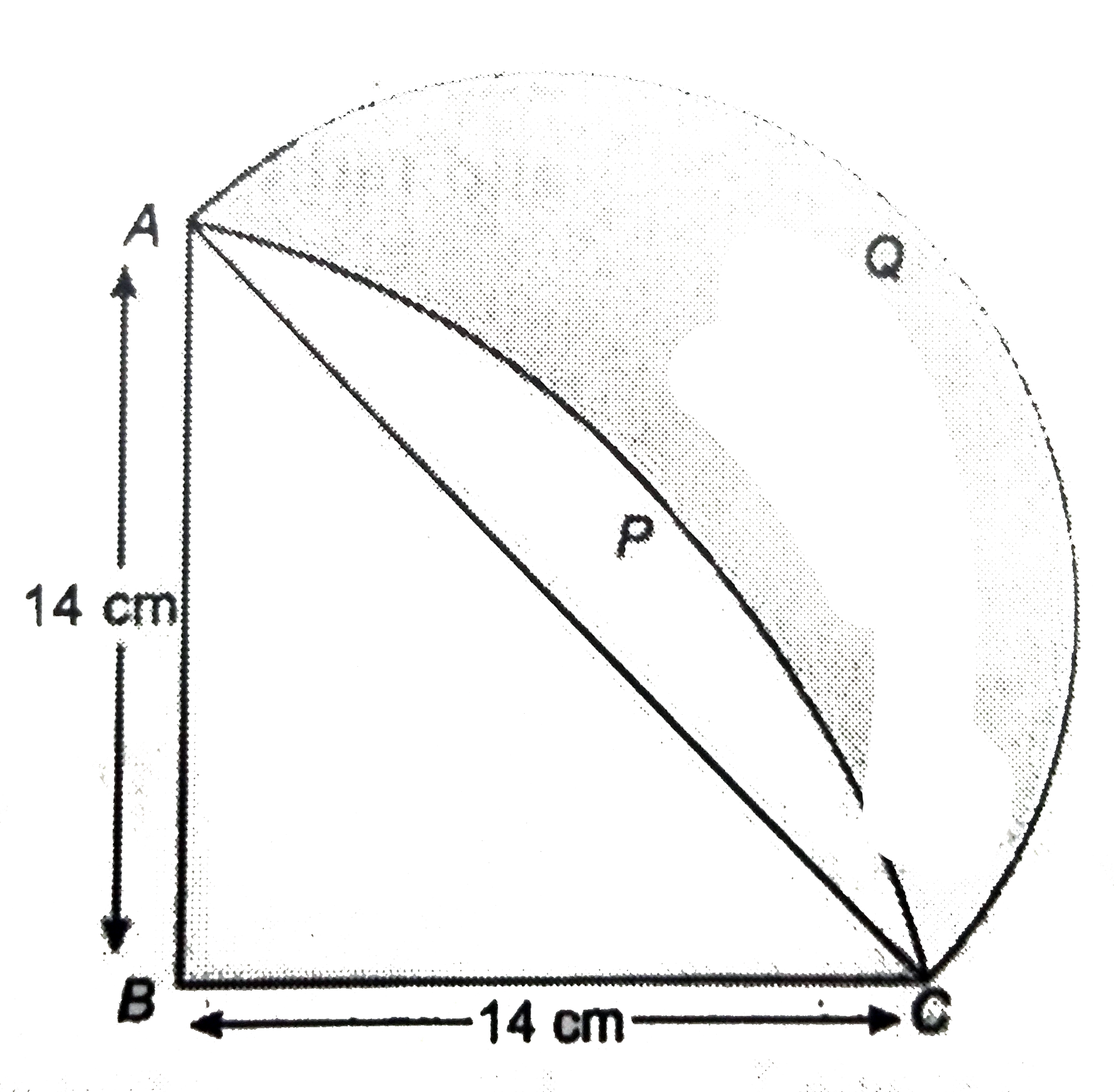
In the right angled-triangle ABC
We have AC2=142+142
⇒AC2=142+142
⇒AC=14√2
⇒AC2=7√2
Area of shaded region = Area of ABCQA - Area of quadrant ABCPA
and area of ABCQA = Area of ΔABC+ Area of semicircle ACQA
Area of quadrant ABCPA =12×(14)2+12×π×(7√2)2=98+154=252cm2
=14×227×(14)2=154cm2
Area of shaded portion =252−154=98cm2
Topper's Solved these Questions
- AREA RELATED TO CIRCLESBOOK - NAGEEN PRAKASHANCHAPTER - AREA RELATED TO CIRCLESEXERCISE - Exercise 12 A
25 Videos
- AREA RELATED TO CIRCLESBOOK - NAGEEN PRAKASHANCHAPTER - AREA RELATED TO CIRCLESEXERCISE - Exercise 12 B
32 Videos
- AREA RELATED TO CIRCLESBOOK - NAGEEN PRAKASHANCHAPTER - AREA RELATED TO CIRCLESEXERCISE - Revision Exercise Long Answer Question
6 Videos
- ARITHMETIC PROGRESSIONBOOK - NAGEEN PRAKASHANCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Revision Exercise Long Answer Question
5 Videos
Similar Questions
Knowledge Check
In the figure, ABC is a right angled triangle with B = 90∘ , BC = 21 cm and AB = 28 cm. With AC as diameter of a semicircle and with BC as radius, a quarter circle is drawn. Find the area of the shaded portion correct to two decimal places
 A428.75cm2B857.50cm2C214.37cm2D371.56cm2
A428.75cm2B857.50cm2C214.37cm2D371.56cm2
In Fig. 12.64, ABCP is a quadrant of a circle of radius 20 cm. With AC as diameter, a semi-cirde is drawn. Find the area of the shaded portion.

View SolutionIn the given figure, ABC is a quadrant of a circle of radius 14 cm and a semicircle is drawn with BC as diameter. Find the area of the shaded region.
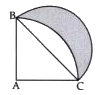
View SolutionIn Fig. 12.33, ABC is a quadrant of a circle of radius 14 cm and a semicircle is drawn with BC as diameter. Find the area of the shaded region.
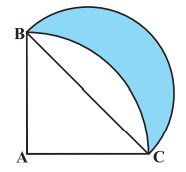
View SolutionIn the given figue, ABCD is a quadrant of a circle of radius 28 cm and a semicircle ABECA is drawn with AC as diameter. Find the area of the shaded region.
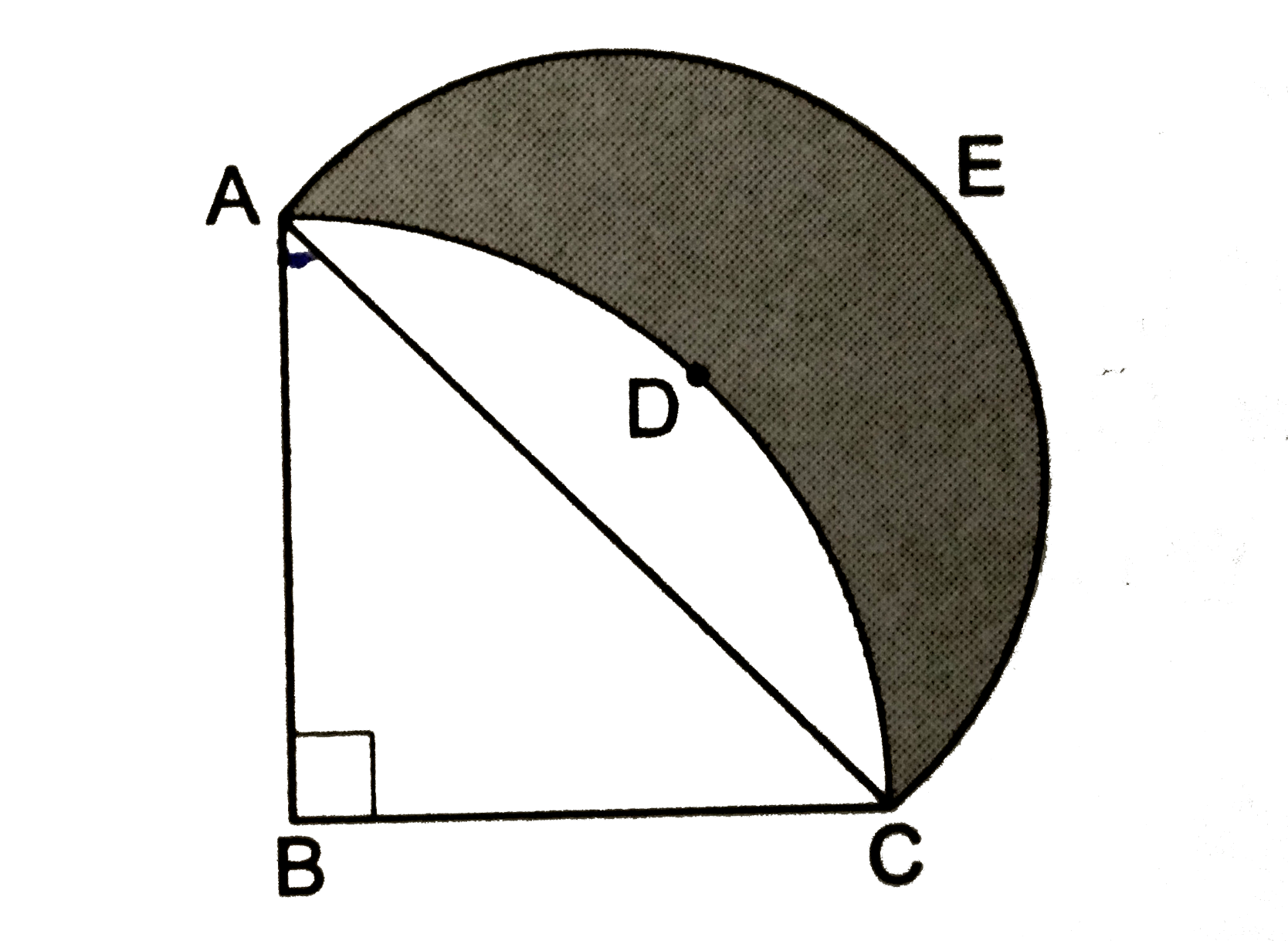
View SolutionIn figure ABDC is a quadrant of a circle of a radius 28 cm and a semi circles BEC is drawn with BC as diameter find the area of shaded region:
View SolutionThe radius of each circle is 'a'. Then the area of the shaded portion is :
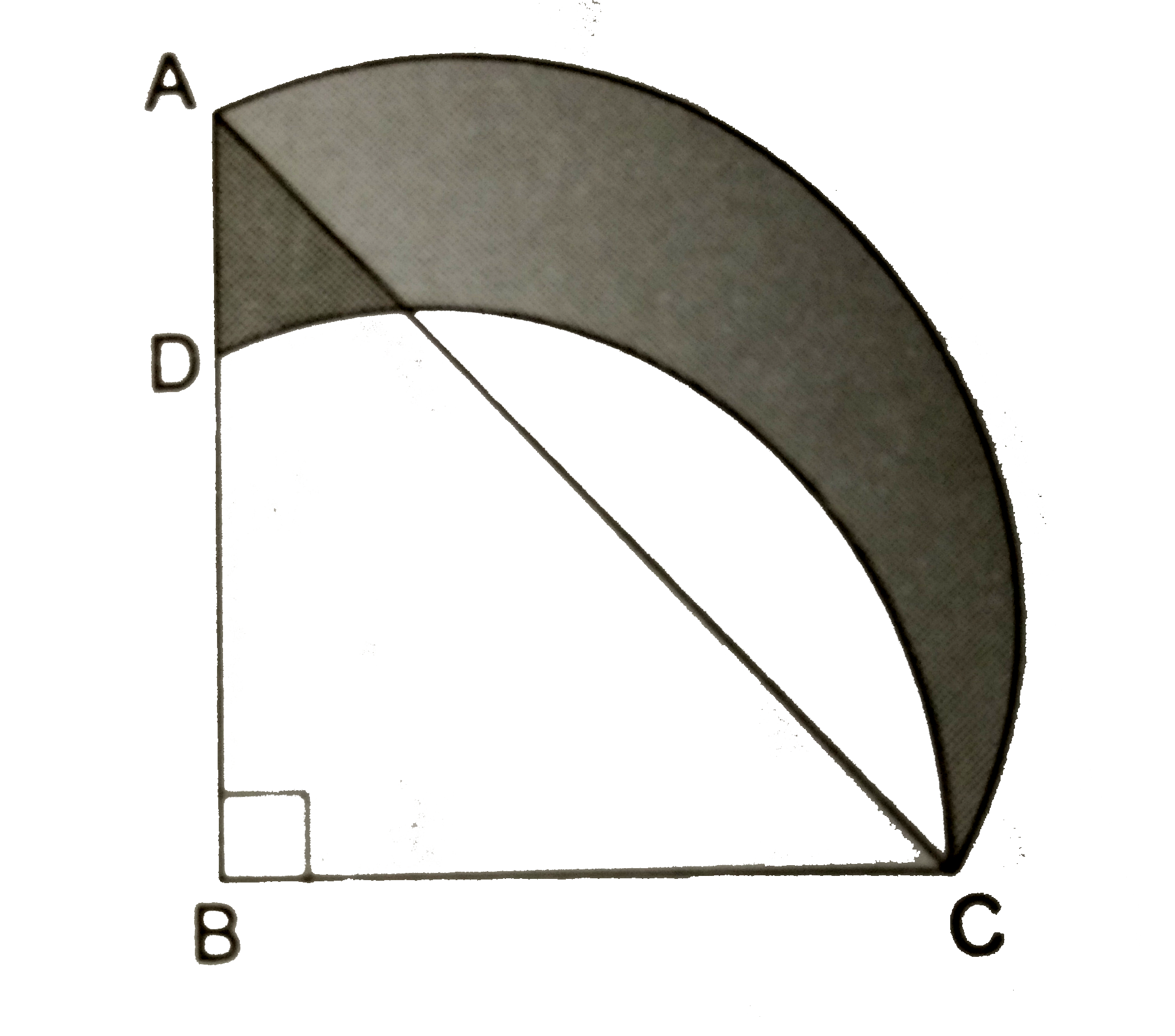
View SolutionIn the given figure ΔABC is a right angled triangle with ∠B=90∘,AB=48cm and BC=14cm. With AC as diameter a semicircle is drawn and with BC as radius, a quadrant of a circle is drawn. Find the area of the shaded region.
[Use π=227]
View Solution
