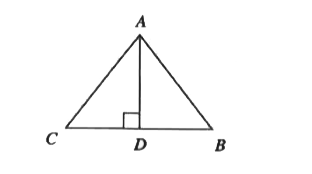
AD is draw perendicular to base BC of an equilateral triangle ABC. Given BC=10 cm find the length of AD, correct to 1 place of decimal.
The correct Answer is:=8.7cm
To find the length of AD in an equilateral triangle ABC where AD is perpendicular to the base BC and BC = 10 cm, we can follow these steps:
Step 1: Understand the properties of the equilateral triangle
In an equilateral triangle, all sides are equal, and the altitude (perpendicular from a vertex to the opposite side) divides the base into two equal parts.
Step 2: Divide the base BC
Since BC = 10 cm, when we draw the perpendicular AD from A to BC, it divides BC into two equal segments:
- BD = DC = 10 cm / 2 = 5 cm
Step 3: Use the Pythagorean theorem
In triangle ABD, we can apply the Pythagorean theorem:
- AB² = AD² + BD²
Step 4: Substitute the known values
Since AB is a side of the equilateral triangle, AB = 10 cm, and BD = 5 cm:
- (10)² = AD² + (5)²
- 100 = AD² + 25
Step 5: Solve for AD²
Rearranging the equation gives us:
- AD² = 100 - 25
- AD² = 75
Step 6: Find AD
Now, take the square root of both sides to find AD:
- AD = √75
- AD = √(25 × 3) = 5√3
Step 7: Calculate the approximate value of AD
To find the numerical value, we can use the approximation √3 ≈ 1.732:
- AD ≈ 5 × 1.732 ≈ 8.66 cm
Step 8: Round to one decimal place
Finally, rounding 8.66 to one decimal place gives us:
- AD ≈ 8.7 cm
Final Answer:
The length of AD is approximately 8.7 cm.
---
In an equilateral triangle, all sides are equal, and the altitude (perpendicular from a vertex to the opposite side) divides the base into two equal parts.
Since BC = 10 cm, when we draw the perpendicular AD from A to BC, it divides BC into two equal segments:
- BD = DC = 10 cm / 2 = 5 cm
In triangle ABD, we can apply the Pythagorean theorem:
- AB² = AD² + BD²
Since AB is a side of the equilateral triangle, AB = 10 cm, and BD = 5 cm:
- (10)² = AD² + (5)²
- 100 = AD² + 25
Rearranging the equation gives us:
- AD² = 100 - 25
- AD² = 75
Now, take the square root of both sides to find AD:
- AD = √75
- AD = √(25 × 3) = 5√3
To find the numerical value, we can use the approximation √3 ≈ 1.732:
- AD ≈ 5 × 1.732 ≈ 8.66 cm
Finally, rounding 8.66 to one decimal place gives us:
- AD ≈ 8.7 cm
The length of AD is approximately 8.7 cm.
Topper's Solved these Questions
- PYTHAGORAS THEORAMBOOK - ICSECHAPTER - PYTHAGORAS THEORAMEXERCISE - EXERCISE 13(B)
18 Videos
- PYTHAGORAS THEORAMBOOK - ICSECHAPTER - PYTHAGORAS THEORAMEXERCISE - QUESTIONS
9 Videos
- MID-POINT THEOREMBOOK - ICSECHAPTER - MID-POINT THEOREMEXERCISE - 4 MARKS QUESTION
15 Videos
- PYTHAGORAS THEOREMBOOK - ICSECHAPTER - PYTHAGORAS THEOREMEXERCISE - 4 MARKS QUESTIONS
9 Videos
Similar Questions
Knowledge Check
What is the area of equilateral triangle if the base BC = 6 ?
 A9√3B18√3C26√3D30√3
A9√3B18√3C26√3D30√3
ΔABC is right-angled at C. If AC=5cmandBC=12cm find the length of AB.
View SolutionIn equilateral △ABC,AD⊥BC and BC=x cm. Find, in terms of x, the length of AD.
View SolutionABC is an isosceles triangle with AB = AC = 2a and BC = a . If AD⊥BC, find the length of AD .
View SolutionFind BC, if the area of the triangle ABC is 36cm2 and the height AD is 3cm (Fing 11.21)
View SolutionAD is an altitude of an equilateral triangle ABC. On AD as base, another equilateral triangle ADE is constructed. Prove that Area ( triangle ADE ): Area ( triangle ABC )=3:4.
View SolutionIn triangle ABC, ∠B=90∘ and tan A = 0.75 If AC = 30 cm, find the lengths of AB and BC.
View Solution△ABC is an isoscles triangle with AB= AC= 13 cm and the length of altitude from A on BC is 5 cm, find BC.
View Solution
