Question

BE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.

Explanation

To prove that triangle ABC is isosceles using the RHS (Right angle-Hypotenuse-Side) congruence rule, we will follow these steps:

Step 1: Identify the Right Triangles
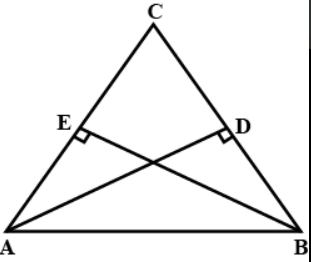
We have triangle ABC with altitudes BE and CF from points B and C to side AC. We will consider the two right triangles:
- Triangle BEC (where BE is the altitude)
- Triangle CFB (where CF is the altitude)

Step 2: Establish Right Angles
Since BE and CF are altitudes, we know that:
- Angle EBF = 90 degrees (BE is perpendicular to AC)
- Angle FCB = 90 degrees (CF is perpendicular to AC)

Step 3: Identify the Common Side
Both triangles BEC and CFB share the side BC. Therefore, we have:
- BC = BC (common side)

Step 4: Use Given Information
According to the problem, the altitudes BE and CF are equal. Thus, we have:
- BE = CF (given)

Step 5: Apply the RHS Congruence Rule
Now we can apply the RHS congruence rule:
- We have two right angles (Angle EBF and Angle FCB are both 90 degrees).
- The hypotenuses (BE and CF) are equal.
- The common side (BC) is equal.

Thus, we can conclude that:
- Triangle BEC is congruent to triangle CFB by the RHS congruence rule.

Step 6: Conclude with Angles
By the property of congruent triangles (CPCTC), we know that:
- Angle BEC = Angle CFB

Since angles opposite to equal sides in congruent triangles are equal, we have:
- Angle B = Angle C

Step 7: State the Isosceles Triangle Property
Since angles B and C are equal, triangle ABC is isosceles by definition (a triangle with at least two equal angles is isosceles).

Conclusion
Therefore, we have proved that triangle ABC is isosceles.

---