CD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of △ABC and △EFG respectively. If △ABC~△FEG, show that :-CDGH=ACFG .Solution in Punjabi
Step by step video & image solution for CD and GH are respectively the bisectors of angleACB and angleEGF such that D and H lie on sides AB and FE of triangleABC and triangleEFG respectively. If triangleABC ~ triangleFEG, show that :-(CD)/(GH)=(AC)/(FG) . by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLESBOOK - SWAN PUBLICATIONCHAPTER - TRIANGLESEXERCISE - EXERCISE 6.4
9 Videos
- TRIANGLESBOOK - SWAN PUBLICATIONCHAPTER - TRIANGLESEXERCISE - EXERCISE 6.5
15 Videos
- TRIANGLESBOOK - SWAN PUBLICATIONCHAPTER - TRIANGLESEXERCISE - EXERCISE 6.2
7 Videos
- SURFACE AREAS AND VOLUMES BOOK - SWAN PUBLICATIONCHAPTER - SURFACE AREAS AND VOLUMES EXERCISE - EXERCISE 13.5(Optional)
7 Videos
Similar Questions
Let ΔABC~ΔDEF and their areas be, respectively, 64 cm2 and 121 cm2. If EF = 15.4 cm, find BC.
View SolutionPQR is a triangle right angled at P and M is a point on QR such that PM ⊥ QR. Show that PM2 = QM.MR.
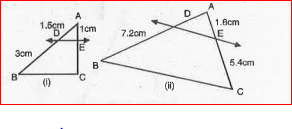
View SolutionIn fig. (i) and (ii), DE || BC. Find EC in (i) and AD in (ii).
 .
.
View SolutionA copper wire 3 mm in diameter is wound about a cylinder whose length is 12 cm, and diameter 10 cm,so as to cover the curved surface of the cylinder. Find the length and mass of the wire, assuming the density of copper to 8.88 g per cm3.
View SolutionCD और GH क्रमशः ∠ACB और ∠EGF के ऐसे समद्विभाजक हैं कि बिन्दु D और H क्रमशः ΔABC और ΔEFG की भुजाओं AB और FE पर स्थित हैं । यदि ΔABC~ΔFEG तो दर्शाइए कि
(i) CDGH=ACFG
(ii) ΔDCB~ΔHGE
(iii) ΔDCA~ΔHGF
View SolutionCD and GH are the bisectors of ∠ACB and ∠EGF respectively. If D lies on AB of ΔABC and H lies on EF of ΔEFG and if ΔABC~ΔEFG, then prove that (a) CDGH=ACFG, (b)ΔDCB~ΔHGE, (c)ΔDCA~ΔHGF
View SolutionCD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ΔABCandΔFEG respectively. IF ΔABC~ΔFEG then show that
CDGH=ACFG
View SolutionCD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ΔABCandΔFEG respectively. IF ΔABC~ΔFEG then show that
ΔDCA~ΔHGF
View SolutionGD and GH are respectively the bisectors of ∠ACBand∠EGF such that D and H lie on sides AB and FE of ΔABCandandΔEFG respectively. If ΔABC~ΔFEG , show that:
CDGH=ACFG
View SolutionGD and GH are respectively the bisectors of ∠ACBand∠EGF such that D and H lie on sides AB and FE of ΔABCandandΔEFG respectively. If ΔABC~ΔFEG , show that:
ΔDCB~ΔHGE
View SolutionGD and GH are respectively the bisectors of ∠ACBand∠EGF such that D and H lie on sides AB and FE of ΔABCandandΔEFG respectively. If ΔABC~ΔFEG , show that:
ΔDCA~De<HGF
View SolutionCD and GH are respectively the bisectors of ⌊ACBand⌊EGF such that D and H lie on sidea AB and FE of ΔABCandΔEFG respectively. If ΔABC~ΔFEG, show that.
i] CDGH=ACFG
ii] ΔCDB~ΔHGE
iii] ΔDCA~ΔHGF
View SolutionCD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ΔABC and ΔEFG respectively. If ΔABC~ΔFEG, show that :
CDGH=ACFG
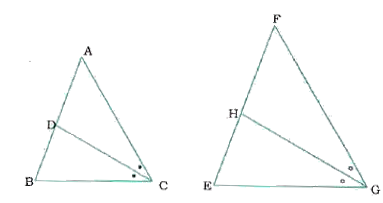
View SolutionCD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ΔABC and ΔEFG respectively. If ΔABC~ΔFEG, show that :
ΔDCB~ΔGHE
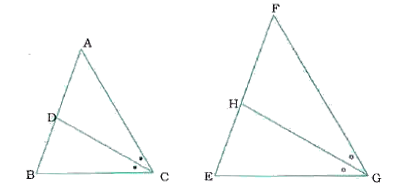
View SolutionCD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ΔABC and ΔEFG respectively. If ΔABC~ΔFEG, show that :
ΔDCA~ΔHGF

View SolutionCD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of △ABC and △EFG respectively. If △ABC~△FEG, show that :-CDGH=ACFG .
View Solution
