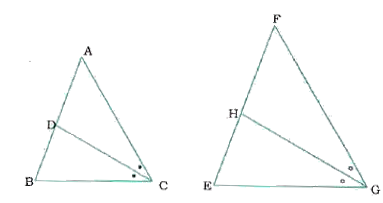
CD and GH are respectively the bisectors of ∠ACBand∠EGFsuch that D and H lie on sides AB and FE of △ABCand△FEG respectively. If △ABC~△FEG.show that:(i)CDGH=ACFGSolution in Assamese
Step by step video & image solution for CD and GH are respectively the bisectors of angleACB and angleEGFsuch that D and H lie on sides AB and FE of triangleABC and triangleFEG respectively. If triangleABC~triangleFEG.show that:(i)(CD)/(GH)=(AC)/(FG) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
All circles are ______ . (congruent, similar)
View Solution2 cubes each of volume 64cm3 are joined end to end.Find the surface area of the resulting cuboid.
View SolutionCD और GH क्रमशः ∠ACB और ∠EGF के ऐसे समद्विभाजक हैं कि बिन्दु D और H क्रमशः ΔABC और ΔEFG की भुजाओं AB और FE पर स्थित हैं । यदि ΔABC~ΔFEG तो दर्शाइए कि
(i) CDGH=ACFG
(ii) ΔDCB~ΔHGE
(iii) ΔDCA~ΔHGF
View SolutionCD and GH are the bisectors of ∠ACB and ∠EGF respectively. If D lies on AB of ΔABC and H lies on EF of ΔEFG and if ΔABC~ΔEFG, then prove that (a) CDGH=ACFG, (b)ΔDCB~ΔHGE, (c)ΔDCA~ΔHGF
View SolutionCD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ΔABCandΔFEG respectively. IF ΔABC~ΔFEG then show that
CDGH=ACFG
View SolutionCD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ΔABCandΔFEG respectively. IF ΔABC~ΔFEG then show that
ΔDCA~ΔHGF
View SolutionGD and GH are respectively the bisectors of ∠ACBand∠EGF such that D and H lie on sides AB and FE of ΔABCandandΔEFG respectively. If ΔABC~ΔFEG , show that:
CDGH=ACFG
View SolutionGD and GH are respectively the bisectors of ∠ACBand∠EGF such that D and H lie on sides AB and FE of ΔABCandandΔEFG respectively. If ΔABC~ΔFEG , show that:
ΔDCB~ΔHGE
View SolutionGD and GH are respectively the bisectors of ∠ACBand∠EGF such that D and H lie on sides AB and FE of ΔABCandandΔEFG respectively. If ΔABC~ΔFEG , show that:
ΔDCA~De<HGF
View SolutionCD and GH are respectively the bisectors of ⌊ACBand⌊EGF such that D and H lie on sidea AB and FE of ΔABCandΔEFG respectively. If ΔABC~ΔFEG, show that.
i] CDGH=ACFG
ii] ΔCDB~ΔHGE
iii] ΔDCA~ΔHGF
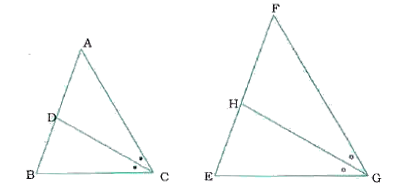
View SolutionCD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ΔABC and ΔEFG respectively. If ΔABC~ΔFEG, show that :
CDGH=ACFG
View SolutionCD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ΔABC and ΔEFG respectively. If ΔABC~ΔFEG, show that :
ΔDCB~ΔGHE
View SolutionCD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ΔABC and ΔEFG respectively. If ΔABC~ΔFEG, show that :
ΔDCA~ΔHGF

View SolutionCD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of △ABC and △EFG respectively. If △ABC~△FEG, show that :-CDGH=ACFG .
View SolutionCD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of △ABC and △EFG respectively. If △ABC~△FEG, show that :- △DCB~△HGE .
View Solution
