CE and DE are equal chords of a cricule with centre O. if ∠AOB=90∘find ar(△CED)ar(△AOB)
Video Solution
Text Solution
Since O is the centre of circle.
∠E=90∘ (angle ina semicircle is right angle)
∠1=∠3(each45∘
△CED~△AOB (AA corollary)
ar(△CED)ar(△AOB)=CD2AB2 ( area ratio theorem)
= (2OB)2OA2+OB2
(CD = diameter and OB= radius so, CD=2 , OB and using pythagoras theorem) .
4OB2OB2+OB2 (OA=OB each radius)
4OB22OB2=21
Hence , ar(△CED)ar(△AOB)=21

|
Topper's Solved these Questions
- TRIANGLES BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLES EXERCISE - Problems From NCERT/ Exemplar
14 Videos
- TRIANGLES BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLES EXERCISE - Exercise 6a
23 Videos
- STATISTICS BOOK - NAGEEN PRAKASHANCHAPTER - STATISTICS EXERCISE - Revision Exercise Long Answer Questions
5 Videos
- VOLUME AND SURFACE AREA OF SOLIDSBOOK - NAGEEN PRAKASHANCHAPTER - VOLUME AND SURFACE AREA OF SOLIDSEXERCISE - Revisions Exercise Long Answer Questions
5 Videos
Similar Questions
Knowledge Check
In the given figure, O is the centre of circle, ∠AOB=100∘. Find ∠BCD :
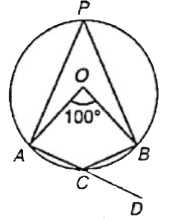 A80∘B60∘C50∘D40∘
A80∘B60∘C50∘D40∘Assertion (A) : PA and PB are triangles to a circle with centre O such that ∠AOB=110∘, then ∠APB=90∘
Reason (R ) : The length of two tangents drawn from an external point are equal .ABoth A and R are true and R is the correct explanation for A.BBoth A and R are true and R is not correct explanation for A.CA is true but R is false.DA is false but R is true.In the given figure, O is the centre of the circle. ∠AOB=70∘, find ∠OCD :
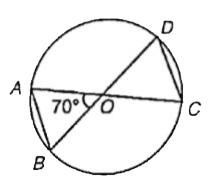 A70∘B55∘C65∘D110∘
A70∘B55∘C65∘D110∘
AB and CD are equal and parallel chords of a circle with centre O. Then AC passes through the centre O. [Agree / Disagree]
View SolutionIf AB, BC and CD are equal chords of a circle with O as centre and AD diameter, then ∠AOB= 600 (b) 900 (c) 1200 (d) none of these
View SolutionIn the given figure, AB and CD are two equal chords. If O is the centre of the circle , ∠AOB=120∘, then find ∠OCD.

View SolutionAB and CD are equal and parallel chords of a circle with centre O. Then AC passes through the centre O. [Agree / Disagree]
View SolutionIn Fig, O is the center of the circle. Find the angle of △ABC.

View Solution