Check if x=2,y=1 is a solution of the system of equations: 3x−2y=4,2x+y=5
The correct Answer is:1
To check if x=2 and y=1 is a solution of the system of equations given by:
1. 3x−2y=4
2. 2x+y=5
we will substitute x and y into both equations and see if they hold true.
Step 1: Substitute x=2 and y=1 into the first equation.
The first equation is:
3x−2y=4
Substituting x=2 and y=1:
3(2)−2(1)=4
Calculating the left-hand side:
6−2=4
This simplifies to:
4=4
This is true.
Step 2: Substitute x=2 and y=1 into the second equation.
The second equation is:
2x+y=5
Substituting x=2 and y=1:
2(2)+1=5
Calculating the left-hand side:
4+1=5
This simplifies to:
5=5
This is also true.
Conclusion
Since both equations are satisfied by x=2 and y=1, we can conclude that (2,1) is indeed a solution of the system of equations.
2. 2x+y=5
3x−2y=4
3(2)−2(1)=4
Calculating the left-hand side:
6−2=4
This simplifies to:
4=4
This is true.
2x+y=5
2(2)+1=5
Calculating the left-hand side:
4+1=5
This simplifies to:
5=5
This is also true.
Topper's Solved these Questions
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 5EXERCISE - PART - A (SECTION - II)20videos
SAMPLE PAPER 5
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 5EXERCISE - PART - B (SECTION - III)8videos
SAMPLE PAPER 5
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 5EXERCISE - SECTION - C10videos
SAMPLE PAPER 5
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 4EXERCISE - PART-B(SECTION-V)5videos
SAMPLE PAPER 4
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 6EXERCISE - SECTION- C10videos
SAMPLE PAPER 6
Similar Questions
Knowledge Check
- Question 1 - Select One
The solution of the system of equations 3x+2y≤12,x≥1,y≤2 is
A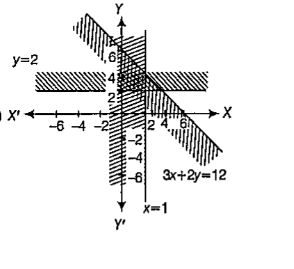 B
B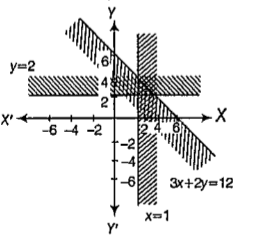 C
C DNone of the above
DNone of the above - Question 2 - Select One
The solution of the system of equations is x−y+2z=1,2y−3z=1 and 3x−2y+4y=2 is
Ax=1,y=5 and z=3Bx=0,y=5 and z=3Cx=0,y=5 and z=−3DNone of the above
If x =α,y=β,z=γ is a solution of the system of equations
x+y+z=4
2x-y+3z=9View SolutionShow tha x=5,y=2 is a solution of the system of linear equation
2x+3y=16,x−2y=1View SolutionFind the solution of the pair of equations :
2x+3y=9
3x+4y=5.View SolutionSolve the system of equations 2x+5y=1 and 3x+2y=7.
View SolutionShow that x=2, y=1 is a solution of the system of simultaneous linear equations: 3x−2y=4; 2x+y=5 .
View SolutionThe solution of system of equations x+y=8,2x−3y=1 is _____and ______
View Solution

