Chords AB and CD intersect at point M inside the circle then theorem of internal division of chords.
AM×BM=□×□
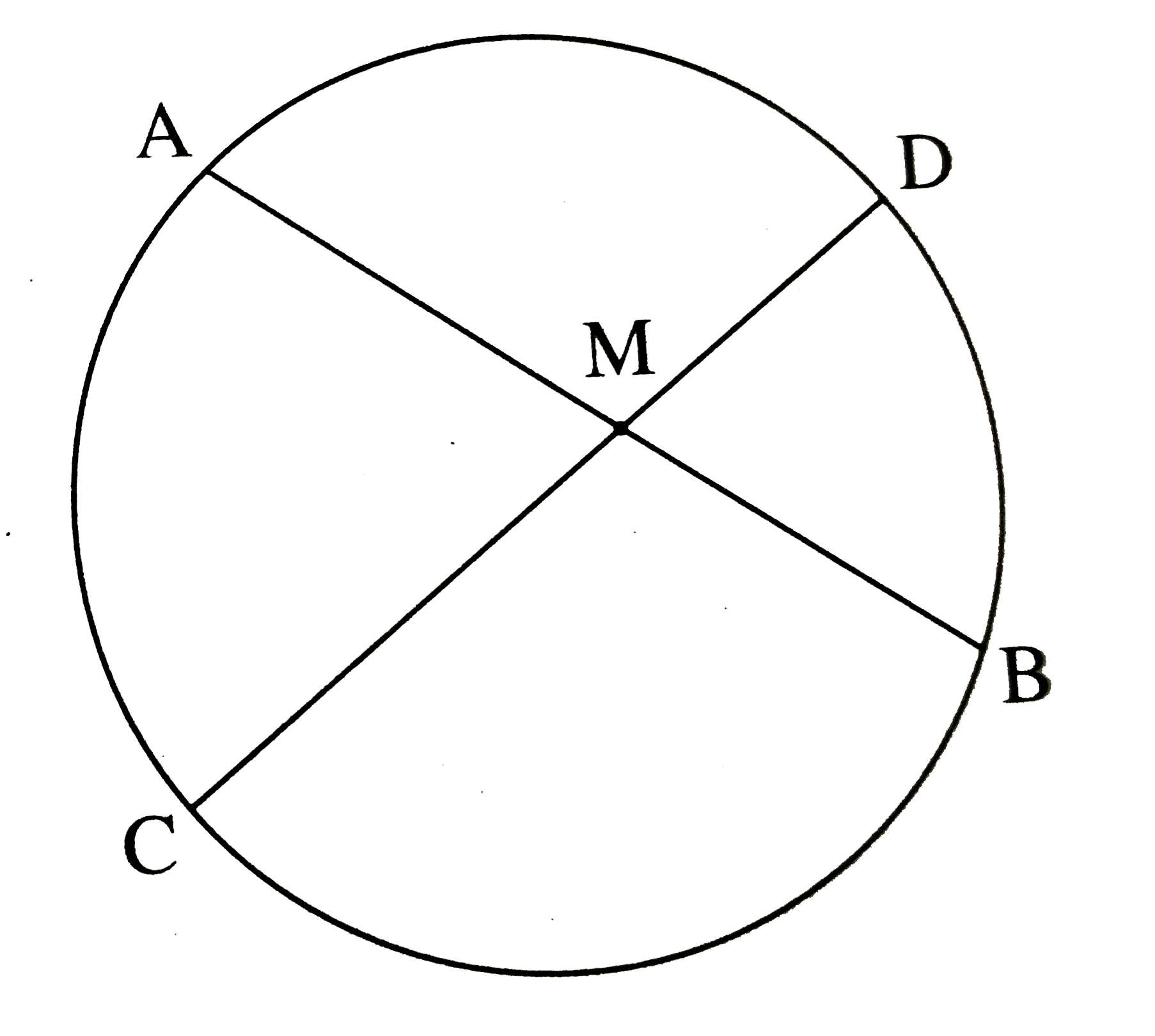
The correct Answer is:AM×MB=CM×DM
Step by step video & image solution for Chords AB and CD intersect at point M inside the circle then theorem of internal division of chords. AM xx BM = square xx square by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - 4.3 (1 mark each)11videos
CIRCLE
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - 4.4 (1 mark each)9videos
CIRCLE
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - Challenging Questions10videos
CIRCLE
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CHALLENGING QUESTIONSEXERCISE - SECTION 3 (MODEL QUESTION PAPER FOR PRACTICE ) Solve any one of the following subquestions :1videos
CHALLENGING QUESTIONS
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - COORDINATE GEOMETRY EXERCISE - Assignment 6.513videos
COORDINATE GEOMETRY
Similar Questions
Knowledge Check
- Question 1 - Select One
Two mutually perpendicular chords AB and CD intersect at point P inside the circle such that CP=15cm.,PD=8cmandPB=6cm. Find the length AC (in cm.)
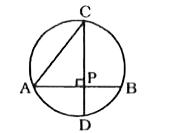 A25B24C20D18
A25B24C20D18 - Question 2 - Select One
Chords AB and CD of a circle intersect at a point P inside the circle. If AB = 10 cm, AP = 4 cm and PC = 5 cm, then CD is equal to:
A4.8 cmB6.8 cmC9.8 cmD7.8 cm - Question 3 - Select One
Vinod have 20 rupees. He bought 1, 2, 5 rupee stamps. They are different in numbers by the reason of no change, the shop keeper gives 3 one rupee stamps. So how many stamps Vinod have ?
AA) 10BB) 18CC) 12DD) 15
In the figure, chord AB and chord CD intersect at point M inside the circle such that AM=4, BM=3, CM=2, then CD=………
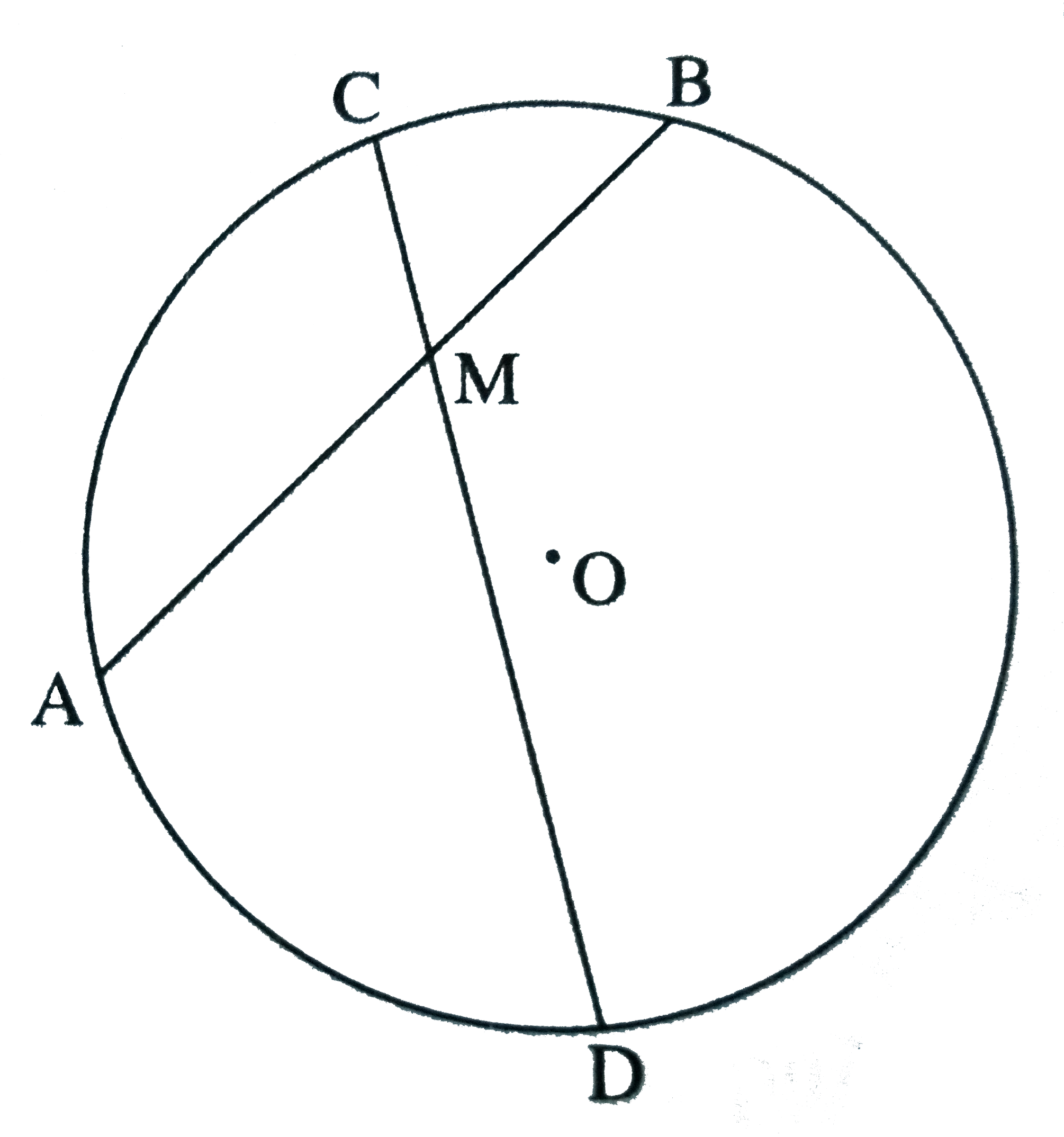 View Solution
View SolutionChord AB and CD intersect each other at point E in the initerior of the circle. In order to prove ∠CEB=12[m(arcAD)+m(arcCB)]
View SolutionTheorem of external division of chords.
If secants containing chords AB and CD of a circle intersect outside the circle in point E, then AE×EB=CE×ED
Given : (1) A circle with centre O
(2) Secants AB and CD intersect at point E outside the circle.
To prove : AE×EB=CE×DE
Construction : Draw seg AD and seg BC
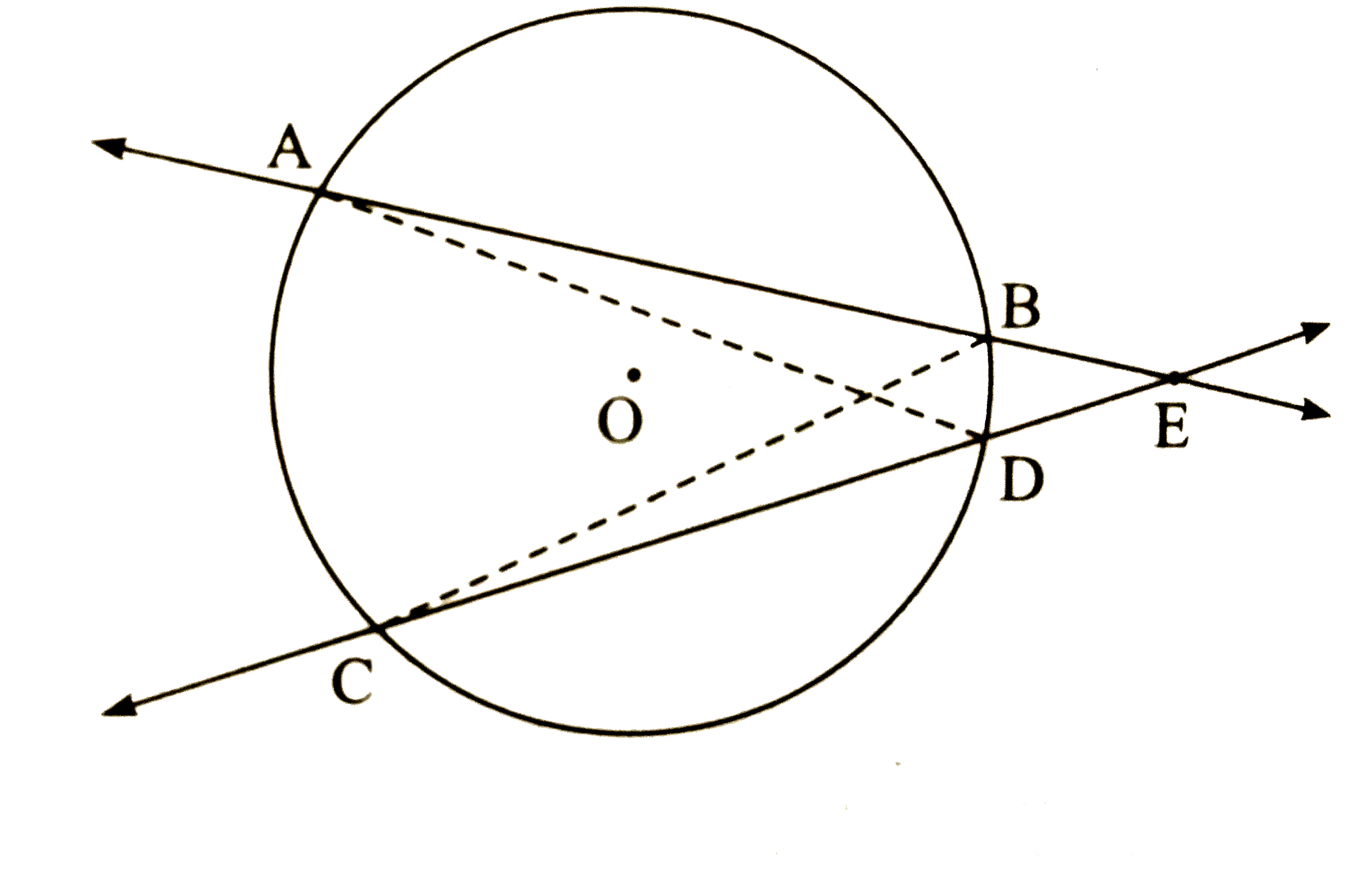 View Solution
View SolutionTheorem of internal division of chords.
Suppose two chords of a circle intersect each other in the interior of the circle, then the product of the lengths of the two segments of one chord is equal to the product of the lengths of the two segments of the other chord.
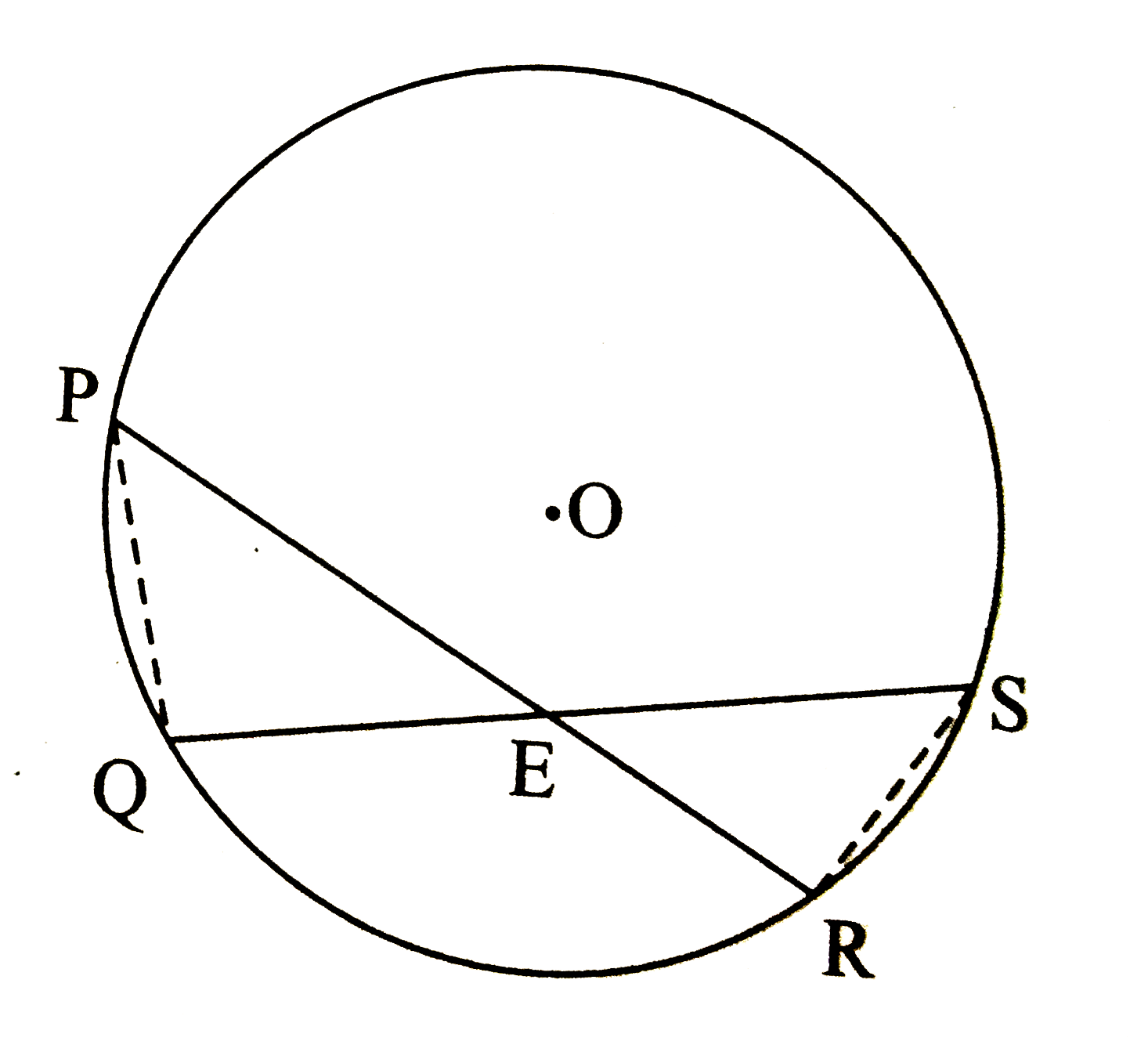
Given : (1) A circle with centre O .
(2) chords PR and QS intersect at point E inside the circle.
To prove : PE × ER = QE xx ES <br>Construction: Draw seg PQ and seg RSView SolutionIn a cricle, two chords AB and CD intersect at a point P inside the circle. Prove that
(a)ΔPAC~ΔPDB (b)PA⋅PB=PC⋅PD.
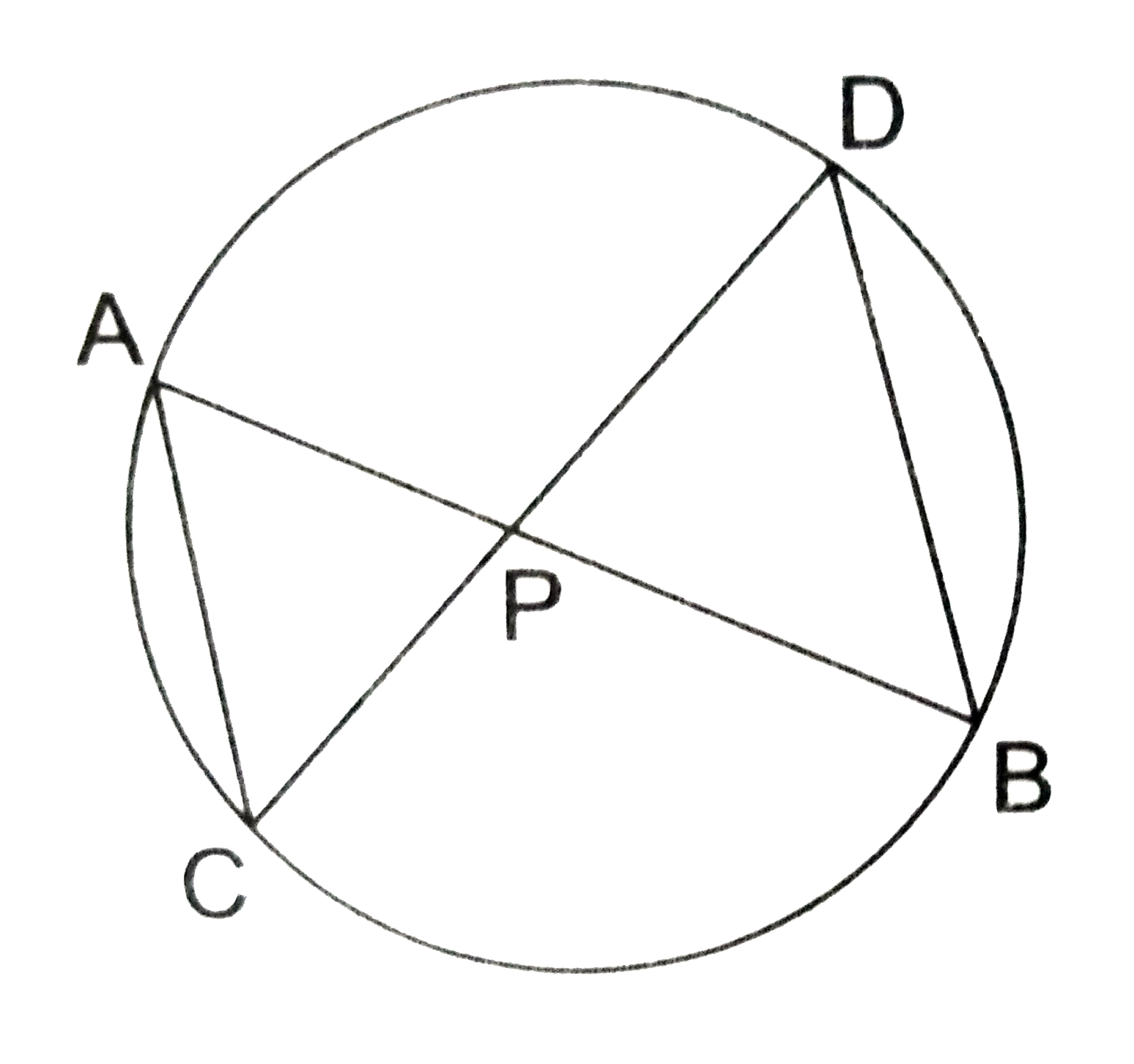 View Solution
View Solution


