Theorem of external division of chords.
If secants containing chords AB and CD of a circle intersect outside the circle in point E, then
Given (1) A circle with centre O
(2) Secants AB and CD intersect at point E outside the circle.
To prove
Construction Draw seg AD and seg BC
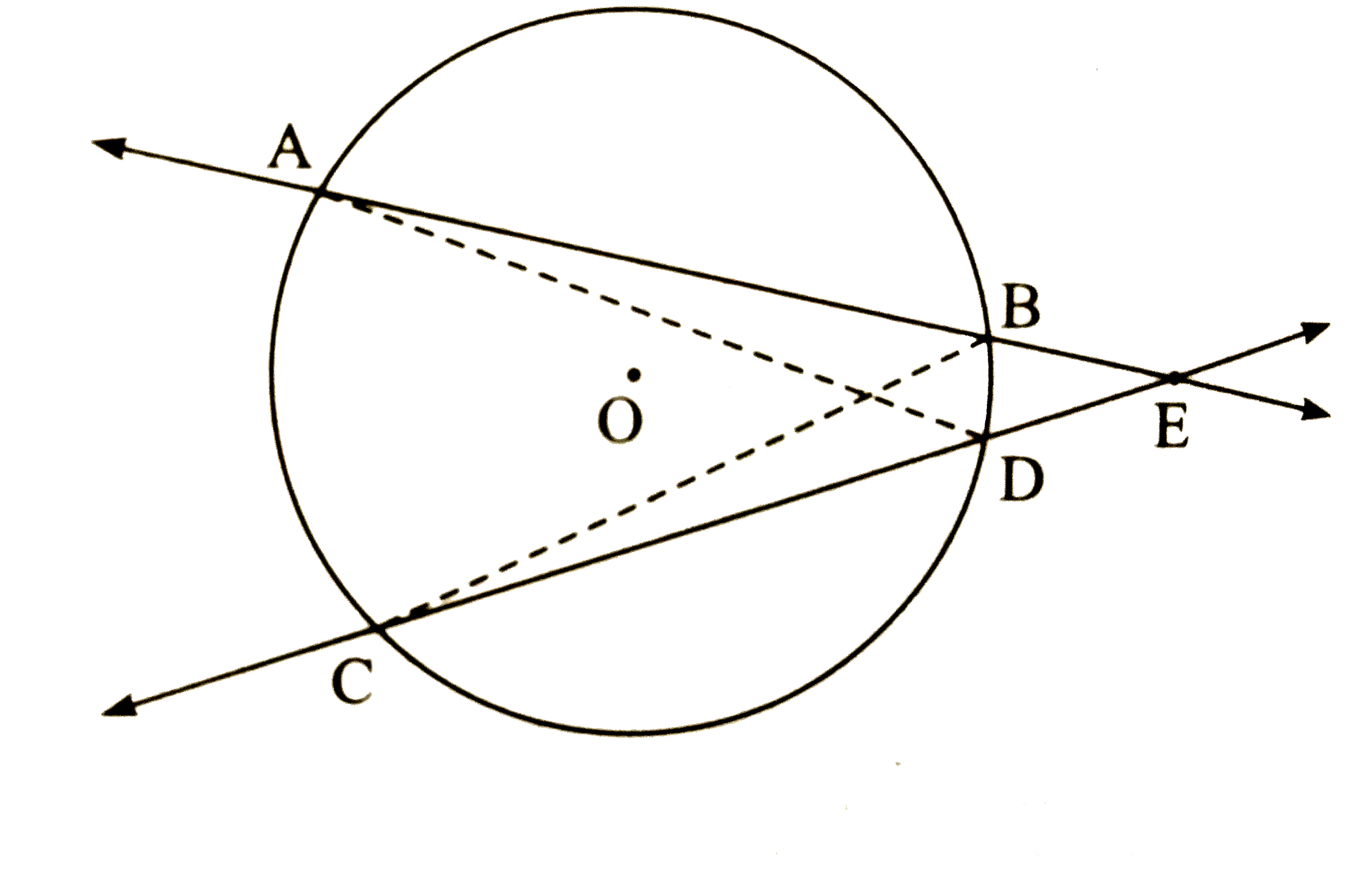
Proof ….(Angles inscribed in the same arc are congruent )
i.e., …(A-B-E and C-D-E ) ….(1)
In and ,
…[From (1)]
....(Common angle)
.....(AA test of similarity )
.... Corresponding sides of similar triangles are in proportion)
.
Topper's Solved these Questions
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - THEOREMS EXERCISE - PYTHAGORAS THEOREM4videos
THEOREMS
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - STATISTICSEXERCISE - EXAMPLES FOR PRACTICE (MCQs)35videos
STATISTICS
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - TRIGONOMETRYEXERCISE - CHALLENGING QUESTIONS6videos
TRIGONOMETRY
Similar Questions
In a circle with centre O, chords AB and CD intersect inside the circumference at E. Prove that ∠AOC+ ∠BOD=2 ∠AEC
View SolutionTheorem of internal division of chords.
Suppose two chords of a circle intersect each other in the interior of the circle, then the product of the lengths of the two segments of one chord is equal to the product of the lengths of the two segments of the other chord.
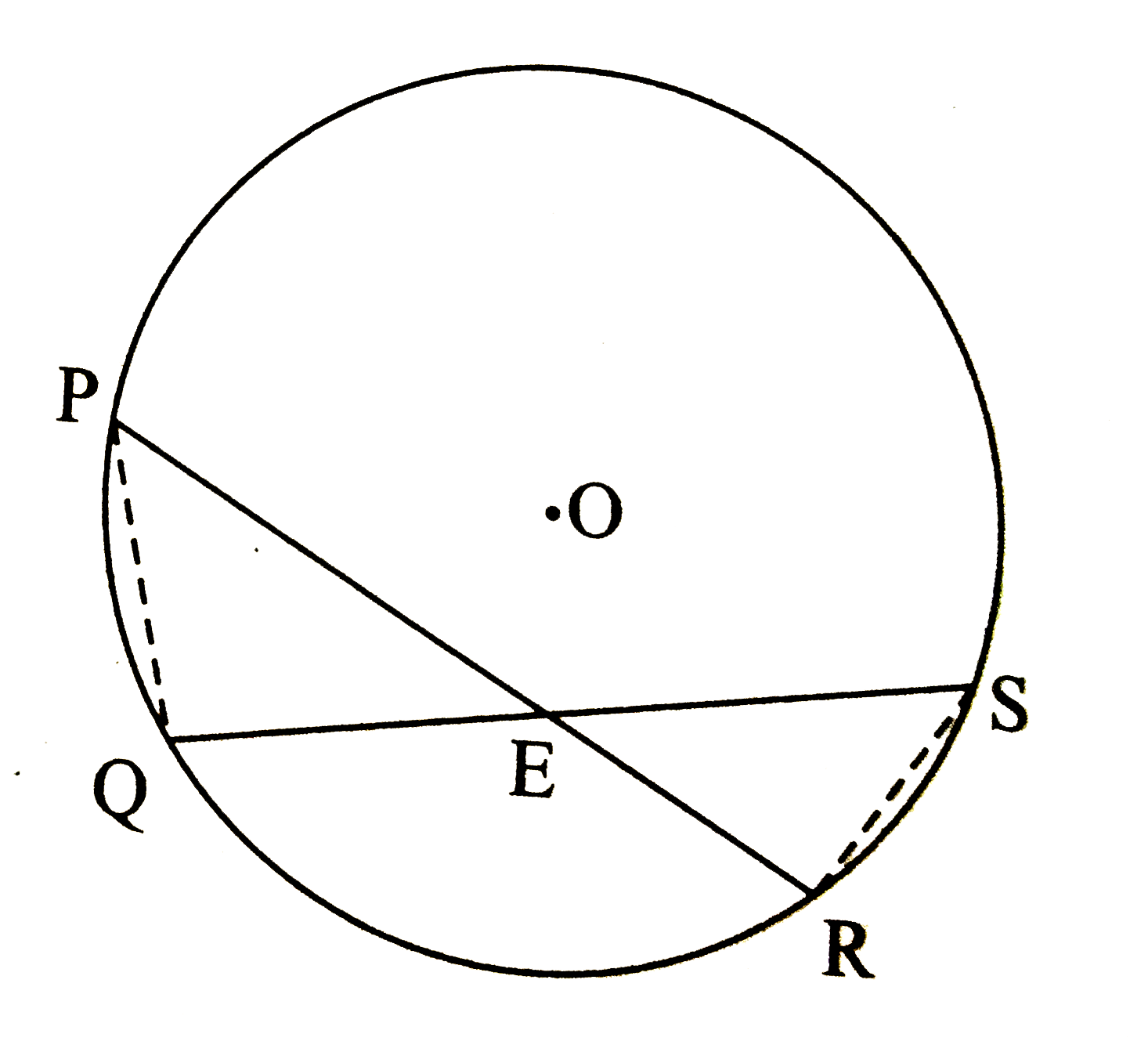
Given : (1) A circle with centre O .
(2) chords PR and QS intersect at point E inside the circle.
To prove : PE × ER = QE xx ES <br>Construction: Draw seg PQ and seg RSView Solution
Knowledge Check
- Question 1 - Select One
Chords AB and CD of a circle interset inside the circle at point E. If AE = 5.6 , EB = 10 cm , CE = 8 ,find ED.
A7B8C11.2D9 - Question 2 - Select One
Two chords AB and CD of a circle with centre O intersect at point P within the circle. ∠AOC+∠BOD=?
A∠APCB2∠APCC32∠APCDNone of these - Question 3 - Select One
Chords AB and CD of a circle intersect at a point P inside the circle. If AB = 10 cm, AP = 4 cm and PC = 5 cm, then CD is equal to:
A4.8 cmB6.8 cmC9.8 cmD7.8 cm
In a circle with centre O, chords ABandCD intersect inside the circumference at E. Prove that ∠AOC+∠BOD=2∠AEC.
View SolutionIn a circle with centre O,chords AB and CD intersect inside the circumference at E.Prove that ∠AOC+∠BOD=2∠AEC
View SolutionTwo chords AB and CD of a circle intersect at a point outside the circle. Prove that
(a)ΔPAC~ΔPDB (b)PA⋅PB=PC⋅PD.
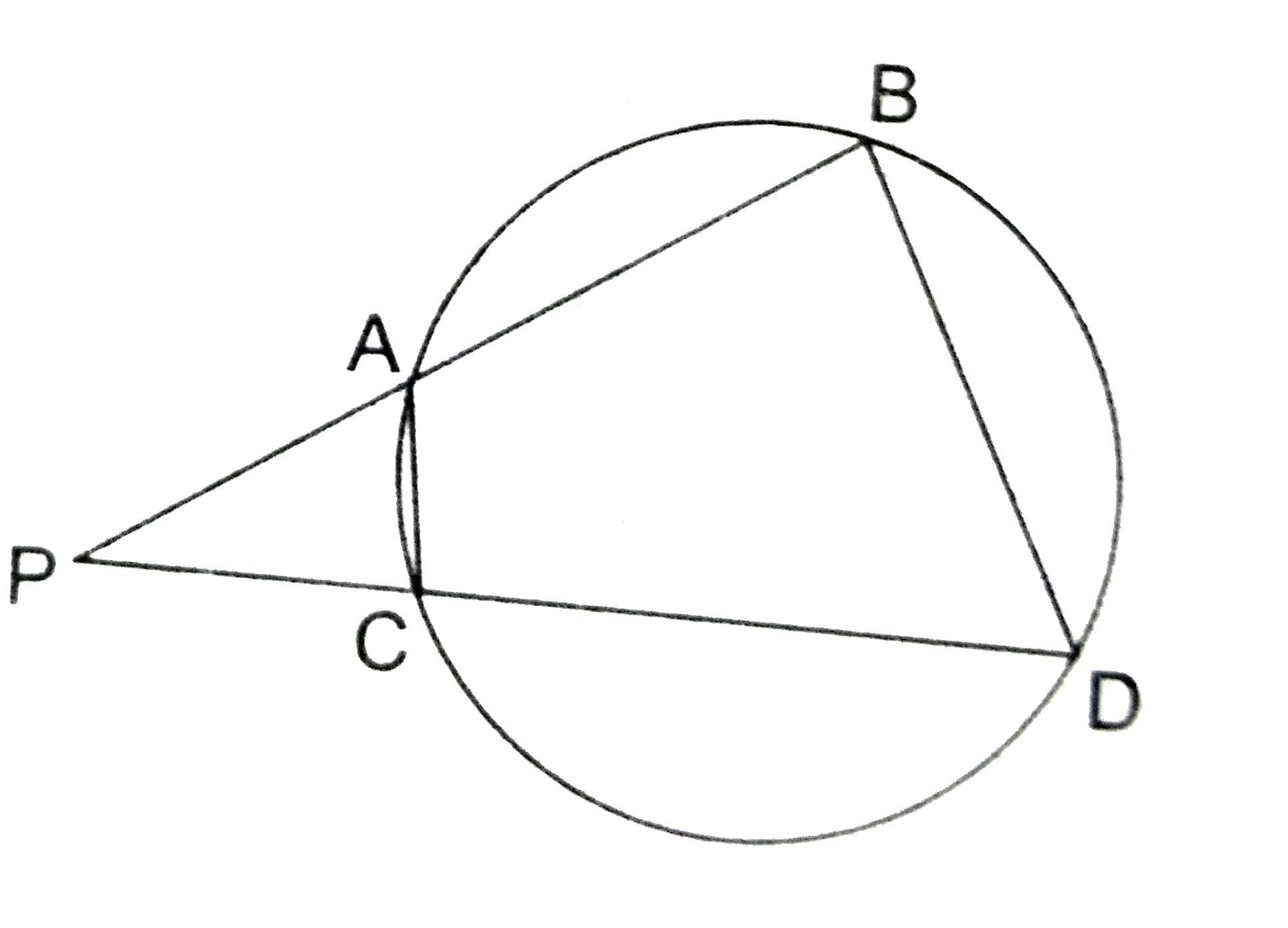 View Solution
View SolutionCommon tangents AB and CD to two circles intersects at E. Prove that AB=CD
View SolutionIn figure, common tangents AB and CD to two circles intersect at E. Prove that AB=CD.
 View Solution
View Solution

