Compute the area of the a surface generated by revolving about the x-axis an are of the curve x=t2,y=t3(t2−3) between the points of intersection of the curve and the x-axis
The correct Answer is:3π
Topper's Solved these Questions
- APPLICATIONS OF THE DEFINITE INTEGRALBOOK - IA MARONCHAPTER - APPLICATIONS OF THE DEFINITE INTEGRALEXERCISE - Geometrical Applications of the Definite Integral
10 Videos
- APPLICATIONS OF THE DEFINITE INTEGRALBOOK - IA MARONCHAPTER - APPLICATIONS OF THE DEFINITE INTEGRALEXERCISE - Computing Pressure, Work and Other Physical Quantities by the Definite Integrals
7 Videos
- APPLICATIONS OF THE DEFINITE INTEGRALBOOK - IA MARONCHAPTER - APPLICATIONS OF THE DEFINITE INTEGRALEXERCISE - The Arc Length of a Curve in Polar Coordinates
7 Videos
- APPLICATION OF DIFFERENTIAL CALCULUS TO INVESTIGATION OF FUNCTIONSBOOK - IA MARONCHAPTER - APPLICATION OF DIFFERENTIAL CALCULUS TO INVESTIGATION OF FUNCTIONSEXERCISE - ADDITIONAL PROBLEMS
9 Videos
- BASIC CLASSES OF INTEGRABLE FUNCTIONS BOOK - IA MARONCHAPTER - BASIC CLASSES OF INTEGRABLE FUNCTIONS EXERCISE - 5.8 INTEGRATION OF OTHER TRANSCENDENTAL FUNCTIONS
5 Videos
Similar Questions
Knowledge Check
If the tangent to the curve x=t2−1,y=t2−t is parallel to x-axis , then
At = 0Bt = 2Ct=12Dt=−12
Compute the area of the curvilinear triangle bounded by the y-axis and the curve, y = tan x and y=(2/3cosx).
View SolutionFind the volume of the solid generated by revolving, about the x-axis, the infinite branch of the curve y=2(1x−1x2)forx≥1.
View SolutionFind the area of the surface obtained by revolving a loop of the curve 9ax2=y(3a−y)2 about the y-axis
View SolutionCompute the length of the loop of the curve x=√3t2,y=t−t3
View SolutionCompute the area of the region enclosed by the curve x=asint,y=bsin2t
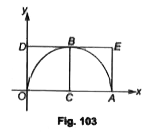
View SolutionGiven: the cycloid x=a(t−sint),y=a(1−cost),0≤t≤2π
Compute. (a) the areas of the surface formed by revolving the arc OBA about the x and y-axis,
(b) the volumes of the solids generated by revolving the figure OBAO about the y-axis and the axis BC,
(c ) the area of the surface generated by revolving the are BA about the axis BC,
(d) the volume of the solid generated by revolving the figure ODBEABO about the tangent line DE touching the figure at the vertex B,
(e ) the area of the surface formed by revolving the are of the cycloid (see item (d)]
View SolutionFind the area enclosed by the loop of the curve , x=t2,y=t−t33
View Solution