Consider f(x)=⎧⎪
⎪⎨⎪
⎪⎩2sin(acos−1x),ifx∈(0,1)√3,ifx=0ax+b,ifx<0
Statement I If b = √3anda=23, then f(x) is continuous in (−∞,1).
Statement II If a function is defined on an interval I and limit exists at every point of interval I, then function is continuous in I. Solution in Punjabi
Statement I is correct, Statement II is also correct, Statement II is the correct explanation of Statement I
Statement I is correct, Statement II is also correct, Statement II is not the correct explanation of Statement I
Statement I is correct, Statement II is incorrect
Statement I is incorrect, Statement II is correct.
The correct Answer is:C
Step by step video & image solution for Consider f(x) = {{:(2 sin (a cos^(-1) x)",","if",x in (0, 1)),(sqrt(3)",","if",x = 0),(ax + b",","if",x lt 0):} Statement I If b = sqrt(3) and a = (2)/(3), then f(x) is continuous in (-oo, 1). Statement II If a function is defined on an interval I and limit exists at every point of interval I, then function is continuous in I. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CONTINUITY AND DIFFERENTIABILITYBOOK - ARIHANT MATHSCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - EXERCISE 4
3 Videos
- CONTINUITY AND DIFFERENTIABILITYBOOK - ARIHANT MATHSCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise (Passage Based Questions)
16 Videos
- CONTINUITY AND DIFFERENTIABILITYBOOK - ARIHANT MATHSCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise (More Than One Correct Option Type Questions)
26 Videos
- COMPLEX NUMBERSBOOK - ARIHANT MATHSCHAPTER - COMPLEX NUMBERSEXERCISE - Complex Number Exercise 8
3 Videos
- COORDINATE SYSTEM AND COORDINATES BOOK - ARIHANT MATHSCHAPTER - COORDINATE SYSTEM AND COORDINATES EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
7 Videos
Similar Questions
A man leaves his home early in the morning to have a walk. He arrives at a junction of roads A and B as shown in figure. He takes the following steps in later journies :
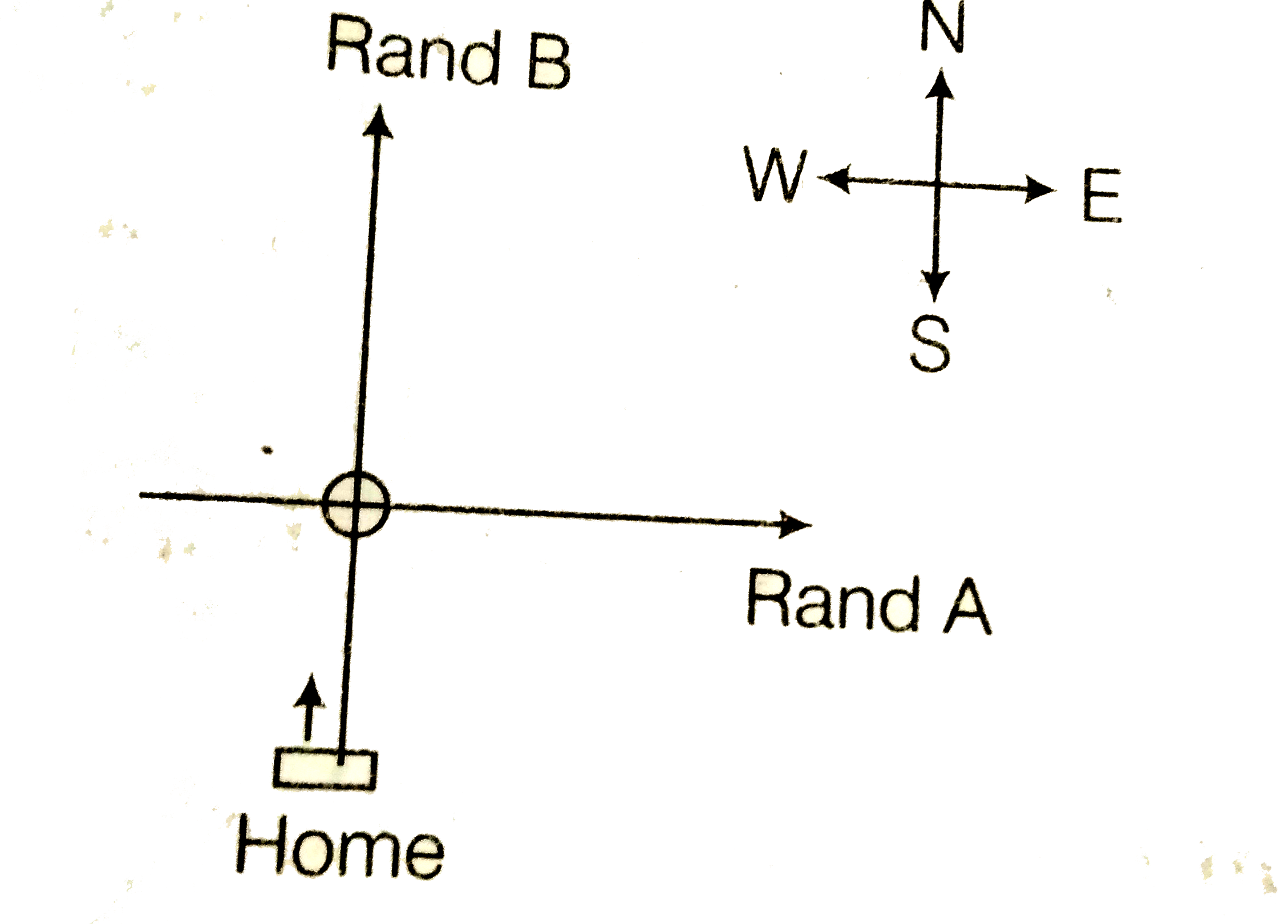
(i) 1 km in North direction.
(ii) Changes direction and moves in North-East direction for 2√2 km.
(iii) Changes direction and moves Southwards for distance of 2 km.
(iv) Finally he changes the direction and moves in South-East direction to reach road A again.
Now if roads A and B are taken as X-axis and y-axis ,then visible point representing the graph of y=f(x)
Then the value of x at which function f(x) is discontinous
View SolutionLet f be a function that is differentiable everywhere and that has the follwong properties :
(i) f(x)>0
(ii) f'(0)=−1
(iii) f(−x)=1f(x)andf(x+h)=f(x).f(h)
A standard result is f'(x)f(x)dx=log|f(x)|+C
The range fo the function Δ=f(|x|) is
View SolutionFunction whose jump (non-negative difference of LHL and RHL) of discontinuity is greater than or equal to one. Is/are
View SolutionFind the modules of 2+3ι
View SolutionIf a vertex of a triangle is (1, 1) and the mid-points of two side through this vertex are (-1, 2) and (3, 2), then centroid of the triangle is
View SolutionA: The functions f(x)=(1+cos^(3)x)/(x^(2))x!=0:f(0)=-(3)/(2) is continuous at x=0R: A function is continuous at x=a if Lt_(x rarr a)f(x)=f(a)
View Solutionf(x)=⎧⎪⎨⎪⎩|x|+3,x≤−3−2x,−3<x<36x+2,x≥3 के सन्दर्भ में निम्नलिखित कथनों पर विचार कीजिए
I. फलन f(x),x=3 पर सतत है ।
II. फलन f(x)=−3 पर सतत है ।
उपरोक्त कथनों में से कौन-सा/से कथन सत्य है/हैं ?
View SolutionConsider f(x)=⎧⎪ ⎪⎨⎪ ⎪⎩2sin(acos−1x),ifx∈(0,1)√3,ifx=0ax+b,ifx<0
Statement I If b = √3anda=23, then f(x) is continuous in (−∞,1).
Statement II If a function is defined on an interval I and limit exists at every point of interval I, then function is continuou in I.
View SolutionLet f(x)=⎧⎨⎩cosx−ex2/2x3,x≠00,x=0, then
Statement I f(x) is continuous at x = 0.
Statement II limx→0cosx−e−x2/2x3=−112
View SolutionI. The function f(x)=√x is continuous at x=0
II. The function f(x)=|x| is continuous at x=0.
View SolutionThe function f(x)=1−cosax1−cosbxfor x≠0,f(0)=ab at x= 0 is
View Solutionअन्तराल ज्ञात कीजिए जिनमे फलन f(x)=(x−1)3(x−2)2 (i) निरन्तर वर्धमान (ii) निरन्तर ह्रासमान है।
View Solutionवक्तव्य I x=2 पर f(x)=√(x−2)+√(2−x) सतत है।
वक्तव्य II f(x) एक बिन्दु फलन है
View Solutionमाना f(x)=⎧⎪ ⎪⎨⎪ ⎪⎩2sin(acos−1x)यदिx∈(0,1)√3यदिx=0ax+bयदिx<0 कथन-I : यदि b=√3 तथा a=23 तो f(x),(−∞,1) में संतत् होगा। क्योंकि
कथन-II : यदि फलन अन्तराल 1 में परिभाषित है तथा अन्तराला के प्रत्येक बिन्दु पर सीमा विद्यमान है, तो फलना में संतत् होगा।
View SolutionIf the function f(x)=1−cos3axxsinx for x≠0f(0)=12 is continuous at x = 0, show that a=±1√3
View SolutionLet f:(−∞,∞)→(−∞,∞) be defined by f(x)=x3+1
Statement - I : The function f has a local exremum at x=0
Statement 2 : The function f is continuous and differentiable on (−∞,∞)andf(0)=0
View Solution
