Doubtnut Promotions Sticky

Consider the following statements
I. If the feasible region of an LPP is undbounded then maximum or minimum value of the obJective function Z = ax + by may or may not exist .
II. Maximum value of the objective function Z = ax + by in an LPP always occurs at only one corner point of the feasible region.
Ill. In an LPP, the minimum value of the objective function Z = ax + by is always 0, if origin is one of the corner point of the feasible region.
IV. In an LPP, the maximum value of the objective function Z = ax + by is always finite.
Which of the following statements are true?

A

I and IV

B

II and III

C

I and III

D

II and IV

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:A

Maximum value of the objective function Z =ax+ by in an LPP may occur at more than one corner points.
∴ Statement II is false Also, in an LPP, since both x and y cannot be zero simultaneously. ∴ Minimum value of the objective function Z = ax + by cannot be 0, if origin is one of the corner point of the feasible solution.
∴ Statement Ill is false.
If the feasible region for LPP is unbounded, then maximum or minimum of the objective function Z = ax + by may or may not exist, statement I is correct.
Also, in an LPP the maximum value of the objective function Z = ax + by is always finite.

|
Updated on:21/07/2023
Class 12MATHSLINEAR PROGRAMMING

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Question 1 - Select One

    Objective function of an LPP is

    Aa constraint
    Ba function to be optimised
    Ca relation between the variables
    Dnone of the above
  • Question 2 - Select One

    In the following the feasible region (shaded) for a LPP is shown Determine the maximum and minimum value of Z=x+2y
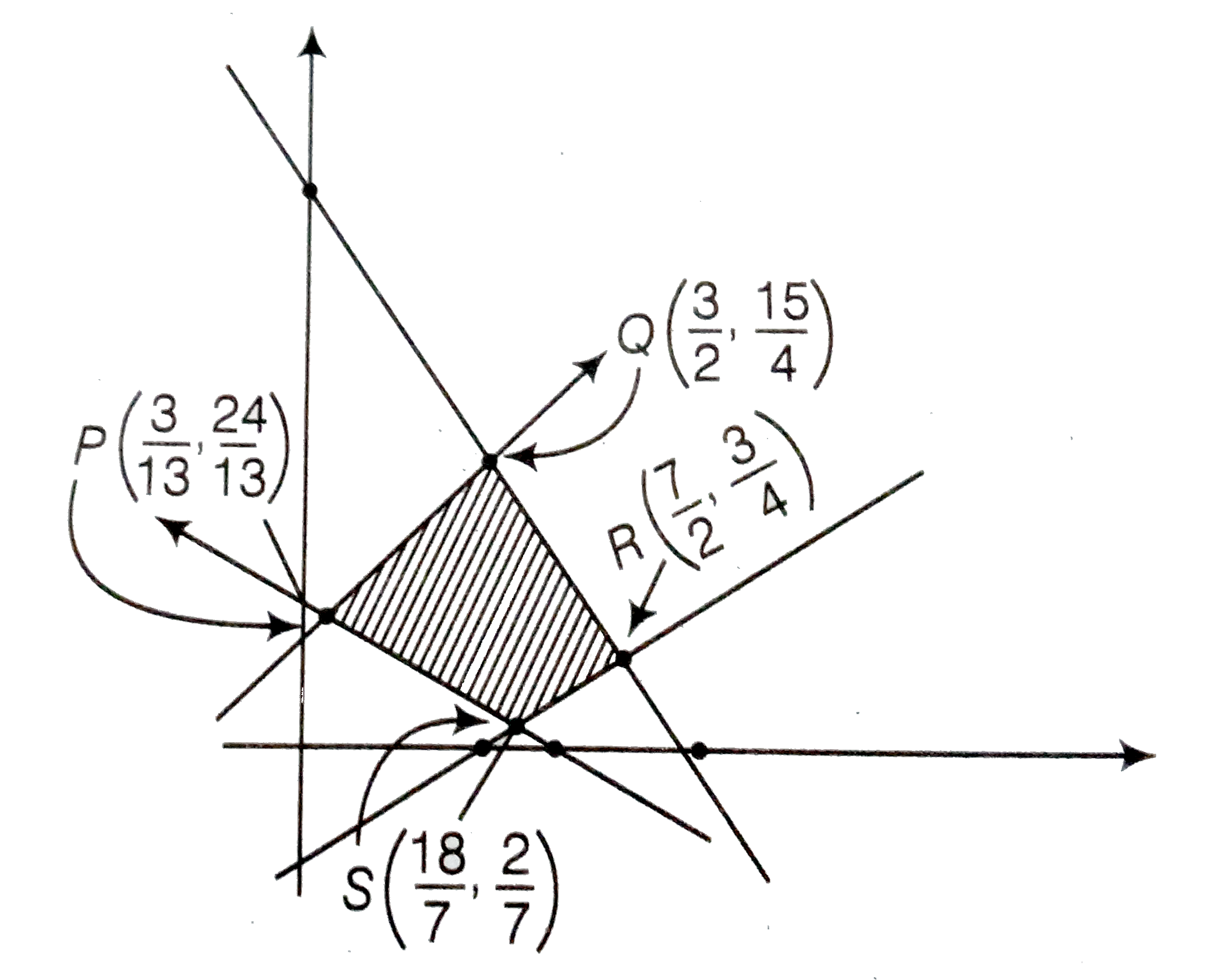    ocr_image

    Amaximum = 7 minimum = 479
    Bmaximum = 9 minimum = 317
    Cmaximum = 10 minimum = 345
    Dmaximum = 8 minimum = 547
  • Question 3 - Select One

    The corner points of the feasible region of an LPP are (0,0),(0,8),(2,7),(5,4) and (6,0). The maximum value of the objective function Z = 3x + 2y is:

    A20
    B23
    C27
    D18