Consider the inequation $x^{2} + x + a - 9 < 0$
The values of the real parameter a so that the given inequations has at least one negative solution.

A

$(- \infty, 9)$

B

$(\frac{37}{4}, \infty)$

C

$(- \infty, \frac{37}{4})$

D

none of these

Video Solution

Text Solution

Verified by Experts

The correct Answer is:3

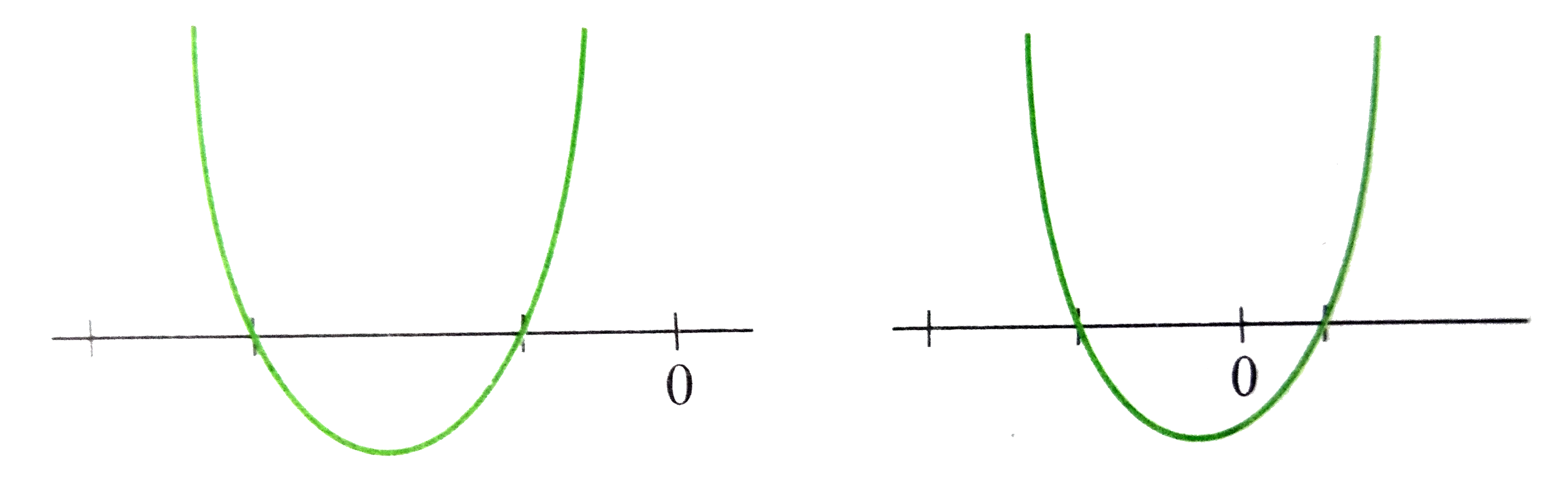
If $x^{2} + x + a - 9 < 0$ has at least one negative solution, then either both the roots of equations $x^{2} + x + a - 9 = 0$ are non-posititve or 0 lies between the roots.
For case I, sum of roots is $a - 9 > 0$
$\Rightarrow a > 9 and$
$D > 0$
$\Rightarrow 1 - 4 (a - 9) > 0 \Rightarrow a < \frac{37}{4}$
Hence, $9 \leq a \leq 37 / 4$ .
For case II, $f (0) > 0$
$\Rightarrow a < 9 \Rightarrow a \in (- \infty, \frac{37}{4})$

Updated on:21/07/2023

|

Class 12 MATHS QUADRATIC EQUATIONS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Consider the inequation $x^{2} + x + a - 9 < 0$
The values of the real parameter a so that the given inequaiton has at least one positive solution:
A $(- \infty, 37 / 4)$
B $(- \infty, \infty)$
C $(3, \infty)$
D $(- \infty, 9)$
Consider the inequation $x^{2} + x + a - 9 < 0$
The value of the parameter a so that the given inequaiton is ture $\forall x \in (- 1, 3)$
A $(- \infty, - 3]$
B $(- 3, \infty)$
C $[9, \infty)$
D $(- \infty, 34 / 4)$
Consider the inequation $9^{x} - a 3^{x} - a + 3 \leq 0$ , where a is real parameter.
The given inequality has at least one negative soluiton for $a \in$
A $(- \infty, 2)$
B $(3, \infty)$
C $(- 2, \infty)$
D $(2, 3)$

CENGAGE-THEORY OF EQUATIONS-Exercise (Comprehension)

Home
Ask Doubt
Profile