Construct, if possible, a quadrilateral ABCD in which AB=6cm, BC=7cm, CD=3cm, AD=5.5cm and AC=11cm. Give reasons for not being able to construct, if you cannot. (Not possible, because in triangle ACD,(AD+CD<AC)
To determine whether we can construct the quadrilateral ABCD with the given side lengths, we will follow these steps:
1. List the Given Measurements:
- AB = 6 cm
- BC = 7 cm
- CD = 3 cm
- AD = 5.5 cm
- AC = 11 cm
2. Identify the Triangles:
- The quadrilateral ABCD can be divided into two triangles: Triangle ACD and Triangle ABC.
3. Check Triangle ACD:
- For triangle ACD, we need to check the triangle inequality theorem, which states that the sum of the lengths of any two sides must be greater than the length of the third side.
- Here, we have:
- AD + CD > AC
- 5.5 cm + 3 cm > 11 cm
- 8.5 cm > 11 cm (This is not true)
4. Conclusion:
- Since the sum of sides AD and CD (8.5 cm) is less than AC (11 cm), triangle ACD cannot be formed.
- Therefore, it is not possible to construct the quadrilateral ABCD with the given measurements.
Reasons for Not Being Able to Construct:
- The construction is not possible because in triangle ACD, the sum of the lengths of sides AD and CD is less than the length of side AC (AD + CD < AC). This violates the triangle inequality theorem.
- AB = 6 cm
- BC = 7 cm
- CD = 3 cm
- AD = 5.5 cm
- AC = 11 cm
- The quadrilateral ABCD can be divided into two triangles: Triangle ACD and Triangle ABC.
- For triangle ACD, we need to check the triangle inequality theorem, which states that the sum of the lengths of any two sides must be greater than the length of the third side.
- Here, we have:
- AD + CD > AC
- 5.5 cm + 3 cm > 11 cm
- 8.5 cm > 11 cm (This is not true)
- Since the sum of sides AD and CD (8.5 cm) is less than AC (11 cm), triangle ACD cannot be formed.
- Therefore, it is not possible to construct the quadrilateral ABCD with the given measurements.
- The construction is not possible because in triangle ACD, the sum of the lengths of sides AD and CD is less than the length of side AC (AD + CD < AC). This violates the triangle inequality theorem.
Topper's Solved these Questions
Similar Questions
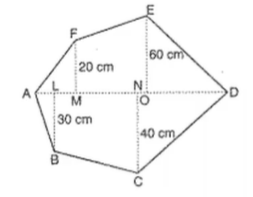
Find the area of the following polygon, if AL=10cm, AM=20cm, AN=50cm, AO=60cm and AD=90cm.
View SolutionIn Fig. 10.57, a circle is inscribed in a quadrilateral ABCD in which ∠B=90o . If AD=23cm , AB=29cm and DS=5cm , find the radius r of the circle. (FIGURE)
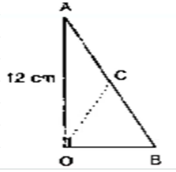
View SolutionIn Figure, ∠AOB=900, AC=BC, OA=12 cm and OC=6.5cm. Find the area of AOB.
View SolutionIn Figure, ABCD is a quadrilateral in which diagonal AC=84 cm ; DL⊥AC, BM⊥AC, DL=16.5 cm and BM=12 cm . Find the area of quadrilateral ABCD.
View SolutionCalculate the area of the quadrilateral ABCD as shown in Fig.33, given that BD=42 cm , AC=28 cm , OD=12 cm and AC⊥BD .
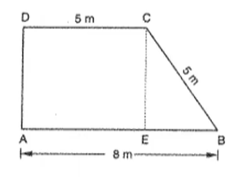
View SolutionIn quadrilateral ABCD show in Figure. ABDC and AD⊥AB. Also, AB=8m, DC=BC=5m. Find the area of the quadrilateral.
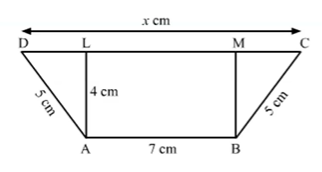
View SolutionIn Figure, ABCD is a trapezium in which AB=7cm, AD=BC=5cm, DC=x cm, and distance between AB and DC is 4cm . Find the value of x and area of trapezium ABCD
View SolutionIn Figure, ABCD is a rectangle with sides AB=10cmandAD=5cm Find the area of EFG

View SolutionIn a parallelogram ABCD diagonals AC and BD intersect at O and AC=6.8 cm and BD=5.6cm . Find the measures of OC and OD
View SolutionIn a ABC , AD is the bisector of ∠BAC . If AB=6cm , AC=5cm and BD=3cm , then DC= 11.3cm (b) 2.5cm (c) 3:5cm (d) None of these
View Solution
