Construct a kite ABCD in which AB=4cm, BC=4.9cm and AC=7.2cm.
Steps of construction :
Step I: Draw AC =7.2cm.
Step II: WithAas the centre and radius 4cm, draw arcs on both sides of the line segment AC
Step III: WithC as the centre and radius4.9cm, draw arcs on both sides of AC iintersecting the previous arcs of step II at BandD.
Step IV Join BA, DA, BC and CD.
Thus, the quadrilateral ABCD so obtained is the required kite.
Topper's Solved these Questions
Similar Questions
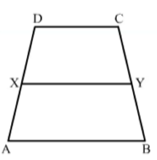
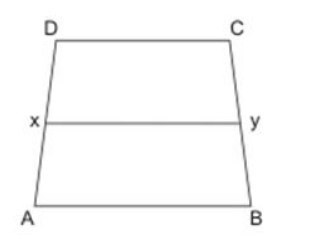
In Figure, ABCD is a trapezium in which AB,DCandDC=40cmandAB=60cm If XandY are, respectively, the mid-points of ADandBC, prove that: ar(traptDCYX)=911,ar(trap(XYBA)
 View Solution
View SolutionIn a ABC, D and E are points on the sides AB and AC respectively. For each of the following cases show that DEBC : AB=10.8cm, BD=4.5 cm, AC=4.8cm and AE=2.8cm (ii) AD=5.7cm, BD=9.5cm, AE=3.3cm and EC=5.5cm .
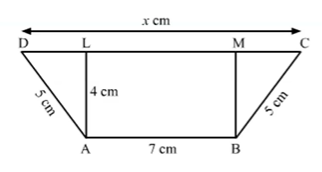
View SolutionIn Figure, ABCD is a trapezium in which AB=7cm, AD=BC=5cm, DC=x cm, and distance between AB and DC is 4cm . Find the value of x and area of trapezium ABCD
 View Solution
View SolutionA paper is in the form of a rectangle ABCD in which AB=20 cm and BC=14 cm. A semicircular portion with BC as diameter is cut off. Find the area of the remaining part.
View SolutionIn Fig. 4.95, if ∠ADE=∠B show that ADE~ABC . If AD=3.8cm , AE=3.6cm , BE=2.1cm and BC=4.2cm , find DE . (FIGURE)
View SolutionIn a triangle, P, Q and R are the mid-points of sides BC, CA and AB respectively. If AC=21 cm, BC=29cm and AB=30cm, find the perimeter of the quadrilateral ARPQ
View SolutionIn a ABC , AD is the bisector of ∠A , meeting side BC at D . If BD=2.5cm, AB=5cm and AC=4.2cm , find DC . (ii) If BD=2cm, AB=5cm and DC=3cm, find AC . (iii) If AB=3.5cm , AC=4.2cm and DC=2.8cm , find BD .
View SolutionIn which of the following cases can a right triangle ABC be constructed? AB=5 cm, BC=7 cm, AC=10 cm AB=7 cm, BC=8 cm, AC=12 cm AB=8 cm, BC=17 cm, AC=15 cm None of these
View SolutionIn Figure, ABCD is a trapezium in which ABDC and DC=40cm and AB=60cm. If X and Y are, respectively, the mid-points of AD and BC , prove that : XY=50cm DCYX is a trapezium ar(trap.DCYX)=911ar(trap.XYBA)
 View Solution
View SolutionIn Fig.42, ABCD is a parallelogram in which AD=21 cm, DH=18 cm and DK=27 cm. The length of side AB is 63 cm (b) 63.5 cm 31.5 cm (d) 31 cm
View Solution

