ΔABC is inscirbed in a circle, the bisector of the angles ∠BAC,∠ABCand∠ACB intersect at the point X,Y,Zon the circle repectively. Prove that in ΔXYZ,∠YXZ=90∘−12∠BAC Solution in Bengali
ΔABC is inscribed in the circle with centre at O. the bisectors of ∠BAC,∠ABCand∠ACB intrsect the circle at the points, X Y and Z respectively. Let us join the point X, Y, Y and, X.
To prove ∠YXZ==90∘−12∠BAC
Proof : ∠AYZand∠ACZ are two angles in circle produced by the are AZ,
∴∠AXZ=∠ACZ.......(1) [ by theorem-35]
Similiarly, ∠AXYand∠ABY are tow angles in circle produced by the are AY.
∴∠AXY=∠ABY......(2) [ by theorem -35]
Now, adding (1) and (2) we get
∠AXZ+∠AXY=∠ACZ+∠ABY
or, ∠YXZ=12∠C+12∠B=12(∠C+∠B)
=12(180∘−∠A)[∴∠A+∠B+∠C=180∘]
=90∘−12∠A=90∘−12∠BAC
Hence ∠YXZ=90∘−12

Topper's Solved these Questions
- THEOREMS RELATED TO ANGLES IN A CIRCLEBOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO ANGLES IN A CIRCLEEXERCISE - EXAMPLES (True or False)
4 Videos
- THEOREMS RELATED TO ANGLES IN A CIRCLEBOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO ANGLES IN A CIRCLEEXERCISE - EXAMPLES (Short-Answer Type Questions) MCQs
5 Videos
- THEOREMS RELATED TO ANGLES IN A CIRCLEBOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO ANGLES IN A CIRCLEEXERCISE - EXAMPLES (Short Answer Type Questions)
5 Videos
- THEOREMS RELATED TO CYCLIC QUADRILATERAL BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO CYCLIC QUADRILATERAL EXERCISE - Long -answer type questions (L.A.)
12 Videos
- THEOREMS RELATED TO TANGENT IN A CIRCLE BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO TANGENT IN A CIRCLE EXERCISE - EXERCISE 4.2
23 Videos
Similar Questions
In the adjoining figure AD and BE are perpendicular ot BC and AC respectively of the ΔABC. The four points A,B,D,E are concylic.
View SolutionIn the adjoining figure, O is the centre of the circle AC is a diameter and chord DE is parallel to the diameter AC. If ∠CBD=60∘ , find the value of ∠CDE
View SolutionIn the adjacent figure O is the centre of the circle. If ∠OAB=30∘,∠ABC=120∘,∠BCO=y∘and∠COA=x∘, then the find value sof x and y.
View SolutionIn a cyclic quadrilateral, the ratio of three consecutive angle is 1 : 2 : 3 Find the value of first and third angles.
View SolutionThe distance of the point from the centre of a circle with diameter of 16 cm is 17 cm. Then the length of the tangent from the point to the circle is
View SolutionANGLES The three angles _BAC_ABCand_ACB are called the angles of ΔABC.
View SolutionThe circumcentre of the triangle ABC is O . Prove that ∠OBC+∠BAC=90∘.
View SolutionTriangle ABC has angle BAC equal to 90∘. What is the measure of the angle ABC? A. The angle ABC is 35∘ B. The angle CBA is 55∘
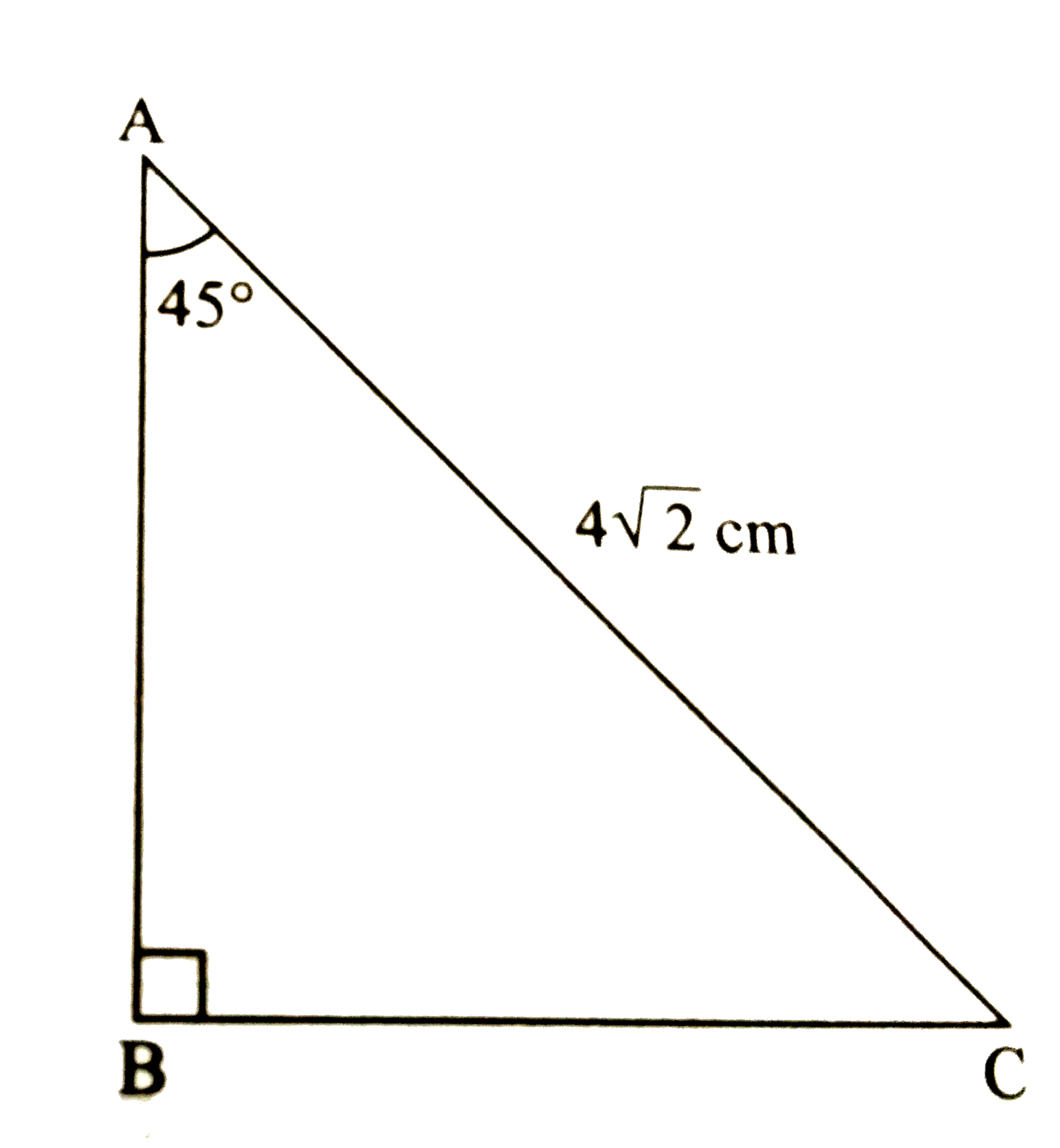
View SolutionIn △ABC,∠ABC=90∘
∠BAC=45∘ and AC =4√2cm,
then find AB.
View SolutionThe triangle ABCis inscribed in a circle, AX, BY and CZ of the angles ∠BAC,∠ABCand∠ACB, intersect at the point X,Y,Z on the circle respectively. Prove that AX is perpendicular to XZ.
View Solutionत्रिभुज ABC में कोण B और C के समद्विभाजक बिंदु O पर काटते है|यदि बढ़ा हुआ AO भुजा BC को P पर काटता हो, तो सिद्ध करो की :
AP,∠BAC का समद्विभाजक है|
View Solution(viii) O is the orthocentre of ΔABC. If ∠BOC=4∠BAC, then find ∠BOCand∠BAC.
View SolutionTwo boys start running at the same time in the same direction at a speed of 10 km/hr and 12 km/hr respectively. In what time they will be 8 km apart?
View SolutionABC is a cyclic triangle and the bisectors of ∠BAC,∠ABCand∠BCA meet the circle at P,Q and R respectively. Then the angle ∠RQP is:
View SolutionIn a triangle aBC ,∠B=2∠C.AD and BE bisectors of ∠BACand∠ABC. If AB=CD . Find ∠BAC
View Solution
