The triangle ABCis inscribed in a circle, AX, BY and CZ of the angles ∠BAC,∠ABCand∠ACB, intersect at the point X,Y,Z on the circle respectively. Prove that AX is perpendicular to XZ. Solution in Bengali
Let ΔABC is inscribed in the circle will centre at O. AX, BY and CZ are the bisectors of ∠BAC,∠ABCand∠ACB respectively and intersect the circle at X,Y and Z respectively.
Let AX,BY and CZ intersect each other at O. Then O is the incentre of the circle. Again let AX intersect YZ at the point E.
To prove : We hve to prove that AX⊥YZi.,AE⊥YZ
∴ are AY are CY[ by the converet of theorem-35]
∴ similarly, are BX= are CX and arc AX= BZ.
[ ∴ angles in the same segment of a cricle are equal]
Again, are AZ and are BZ produced two equal central angles.
∴∠AOX=∠BOZ.......(1)
Similary ∠AOY=∠COY[∴ AY = are CY]
or,∠AOY=∠BOZ[ oppoiste angles]....(2)
∴∠AOZ=∠AOYor,∠EOZ=∠EOY.......(3)
Bow, in ΔEOYandΔEOZ,OY=OZ(∴ radii of same circle,)
∠EOY=∠EOZ [ from (3) ] and OE is common to both.

∴ΔEPO≅ΔEOZ [ by the S-A-S conditino of congreuency]
∠OEY=∠OEZ[∴ similar angles of congruent triangles]
But these two angles are adjustment obtained when the line segment OE stands upon the line segment YZ and they are equal.
∴ each is right angle i.e., ∠OEY=∠OEZ= right angle.
∴OE⊥orAX⊥YZ ltbr ∴ Ax is perpendicular to YZ
Topper's Solved these Questions
- THEOREMS RELATED TO ANGLES IN A CIRCLEBOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO ANGLES IN A CIRCLEEXERCISE - EXAMPLES (True or False)
4 Videos
- THEOREMS RELATED TO ANGLES IN A CIRCLEBOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO ANGLES IN A CIRCLEEXERCISE - EXAMPLES (Short-Answer Type Questions) MCQs
5 Videos
- THEOREMS RELATED TO ANGLES IN A CIRCLEBOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO ANGLES IN A CIRCLEEXERCISE - EXAMPLES (Short Answer Type Questions)
5 Videos
- THEOREMS RELATED TO CYCLIC QUADRILATERAL BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO CYCLIC QUADRILATERAL EXERCISE - Long -answer type questions (L.A.)
12 Videos
- THEOREMS RELATED TO TANGENT IN A CIRCLE BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO TANGENT IN A CIRCLE EXERCISE - EXERCISE 4.2
23 Videos
Similar Questions
In the adjoining figure AD and BE are perpendicular ot BC and AC respectively of the ΔABC. The four points A,B,D,E are concylic.
View SolutionIn the adjoining figure, O is the centre of the circle AC is a diameter and chord DE is parallel to the diameter AC. If ∠CBD=60∘ , find the value of ∠CDE
View SolutionIn the adjacent figure O is the centre of the circle. If ∠OAB=30∘,∠ABC=120∘,∠BCO=y∘and∠COA=x∘, then the find value sof x and y.
View SolutionIn a cyclic quadrilateral, the ratio of three consecutive angle is 1 : 2 : 3 Find the value of first and third angles.
View SolutionThe distance of the point from the centre of a circle with diameter of 16 cm is 17 cm. Then the length of the tangent from the point to the circle is
View SolutionABC is a right angle triangle right angled at A. A circle is inscribed in it the length of the two sidescontaining right angle are 6cm and 8cm then the radius of the circle is
View SolutionANGLES The three angles _BAC_ABCand_ACB are called the angles of ΔABC.
View SolutionIf a circle is inscribed in right angled triangle ABC with right angle at B, show that the diameter of the circle is equal to AB+BC−AC.
View SolutionThe circumcentre of the triangle ABC is O . Prove that ∠OBC+∠BAC=90∘.
View SolutionO is the circumcentre of ΔABC and OD is perpendicular on the side BC, prove that ∠BOD=∠BAC
View SolutionΔABC is inscirbed in a circle, the bisector of the angles ∠BAC,∠ABCand∠ACB intersect at the point X,Y,Zon the circle repectively. Prove that in ΔXYZ,∠YXZ=90∘−12∠BAC
View SolutionThe isosceles triangle ABC is inscribed in a circle with centre at O. If AP is a diameter of the circle. Then prove that AP is the bisetors of ∠BPC.
View SolutionTriangle ABC is inscribed in a circle, such that AC is a diameter of the circle and angle BAC is 45∘. If the area of triangle ABC is 72 square units, how larger is the area of the circle than the area of triangle ABC ?
View SolutionABC is a right angle triangle right angled at A. A circle is inscribed in it the length of the two sidescontaining right angle are 6 cm and 8 cm then the radius of the circle is
View SolutionIn the figure, O is centre of a circle. If ∠BAC=20∘and∠ACB=30∘. Find ∠AOC
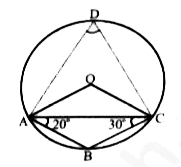
View Solution
