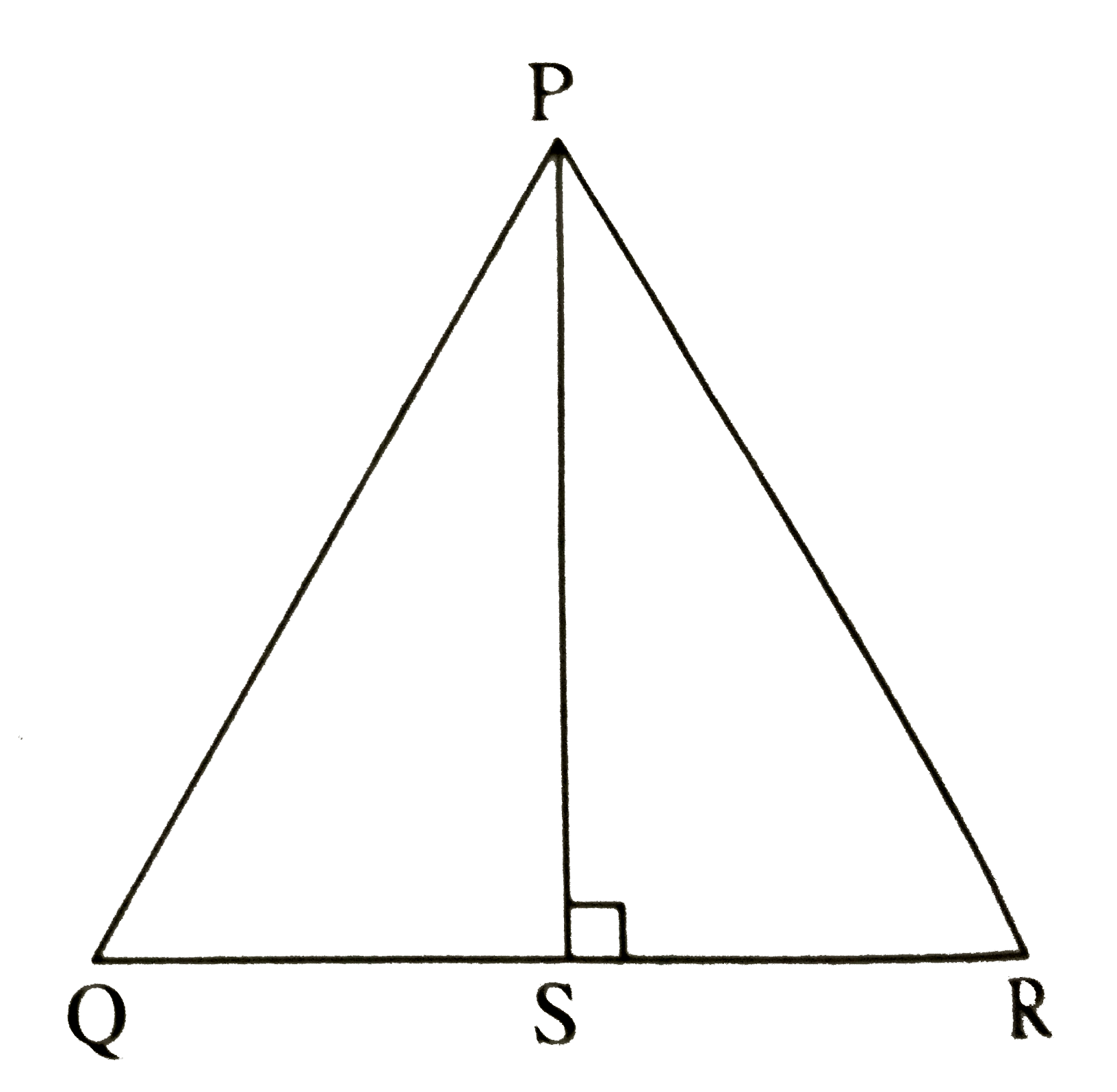
ΔPQR is an equilateral triangle. Seg PS⊥ side QR such that Q−S−R. Prove PS2=3QS2 by completing the following activity.
In ΔPQS,
∠PSQ=□……(Given)
∠Q=□………….(Angle of an equilateral triangle)
∴∠QPS=30∘.................(Remaining angle of ΔPQS)
∴ΔPQS is a □ triangle
PS=□PQ.............(Side opposite to 60∘)..............(1)
and QS=□PQ..........(Side opposite to 30∘)
PQ=2QS .....(2)
Substituting value of PQ from (2) in (1)
PS=√32×2QS
∴PS=□QS
∴PS2=3QS2......(Square both the sides)
4QS2
3QS2
32QS2
2QS2
The correct Answer is:B
Step by step video, text & image solution for DeltaPQR is an equilateral triangle. Seg PS bot side QR such that Q-S-R. Prove PS^(2)=3QS^(2) by completing the following activity. In DeltaPQS, /_PSQ=square……(Given) /_Q=square………….(Angle of an equilateral triangle) :. /_QPS=30^(@).................(Remaining angle of DeltaPQS) :.DeltaPQS is a square triangle PS=square PQ.............(Side opposite to 60^(@))..............(1) and QS=square PQ..........(Side opposite to 30^(@)) PQ=2QS .....(2) Substituting value of PQ from (2) in (1) PS=(sqrt(3))/(2)xx2QS :.PS=square QS :.PS^(2)=3QS^(2)......(Square both the sides) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - PYTHAGORAS THEOREMEXERCISE - EXAMPLES FOR PRACTICE (2 MARK QUESTIONS )9videos
PYTHAGORAS THEOREM
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - PYTHAGORAS THEOREMEXERCISE - EXAMPLES FOR PRACTICE ( 3 MARK QUESTIONS )8videos
PYTHAGORAS THEOREM
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - PYTHAGORAS THEOREMEXERCISE - Assignment 3.55videos
PYTHAGORAS THEOREM
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - PROBABILITY EXERCISE - ASSIGNEMENT 5.412videos
PROBABILITY
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUADRATIC EQUATION EXERCISE - CHALLENGIN QUESTIONS2videos
QUADRATIC EQUATION
Similar Questions
Knowledge Check
- Question 1 - Select One
The ratio of the area of a square of side a and that of an equilateral triangle of side a, is
A2 : 1B2:√3C4 : 3D4:√3
If Q is a point on the side SR of a triangle PSR such that PQ=PR then prove that PS>PQ
View SolutionIn the adjoining figure, ΔPQR is an equilateral triangle. Point S is on seg QR. such that QS=13QR. Prove that : 9PS2=7PQ2.
View SolutionIn ΔPQS,RT⊥QS. Find a and b.
View SolutionIn ΔPQR, if S is any point on side QR, show that PQ+QR+RP>2PS.
View SolutionIn an isosceles triangle PQR, PQ =PR and S is any point on side QR. Then prove that: PQ2−PS2=QS×SR.
View SolutionIn trapezium PQRS, side PQ∣∣ side SR, AR=5AP, AS=5AQ then prove that SR=5PQ by completing the following activity.
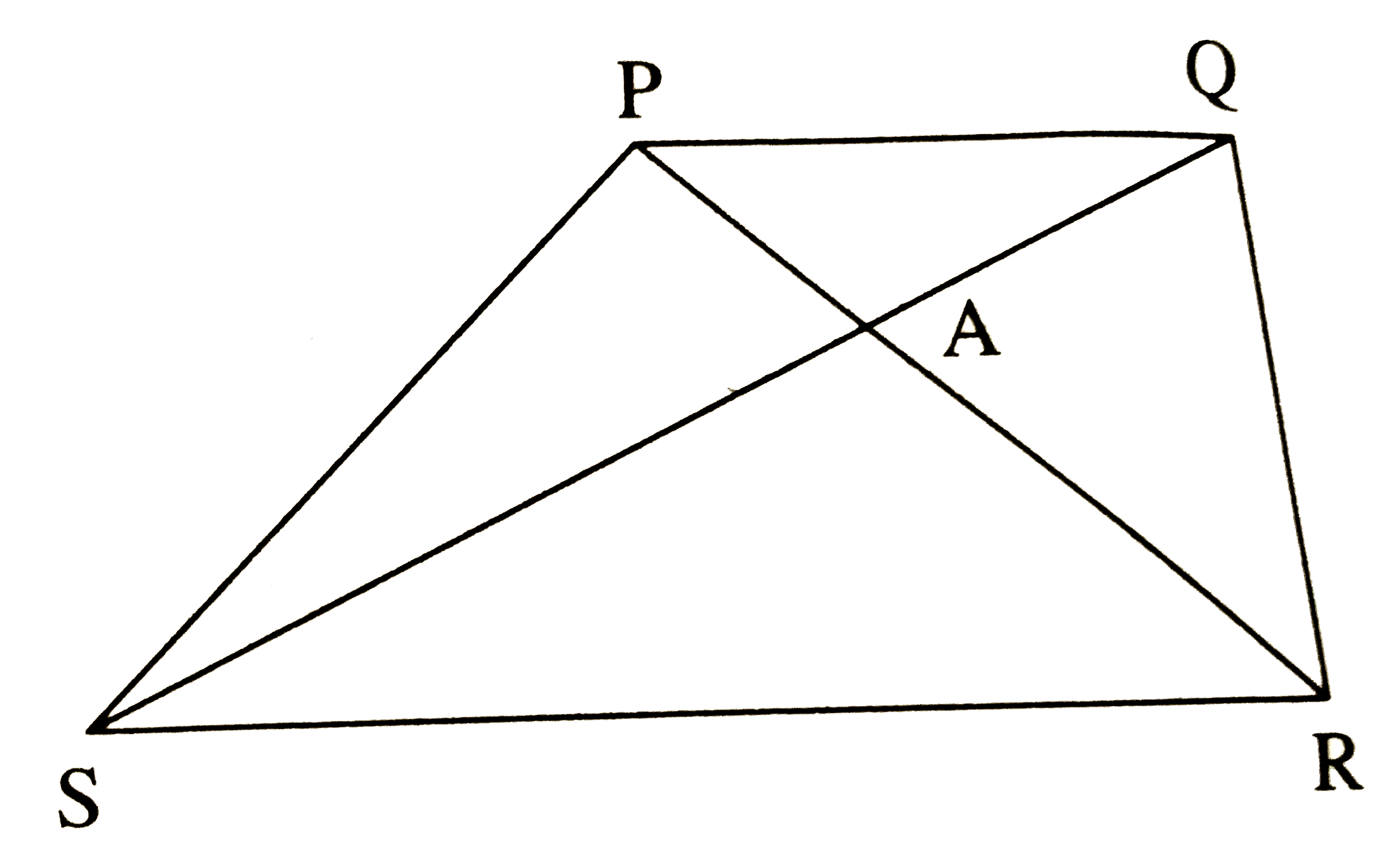
In ΔPQA and ΔRSA,
∠PQA≅∠RSA……(□)
∠PAQ≅∠RAS....(□)
∴ΔPQA~ΔRSA ......(□)
PQSR=□AR.........(Corresponding sides of similar triangles).....(1)
Substituting AR=5AP in (1)
∴PQSR=□5AP
∴PQSR=□5
∴SR=5PQView SolutionIn PQR , S is any point on the side QR . Show that PQ+QR+RP>2PS
View Solution


