Determine a point which divides a line segment 7 cm long, internally in the ratio 2:3
1. Draw a line segment AB=7cm by using a ruler.
2. Draw any ray making an acute ∠BAC with AB.
3. Along AC, mark off (2+3)=5 point A1,A2,A3,A4 and A5 such that
AA1=A1A2=A2A3=A3A4=A4A5.
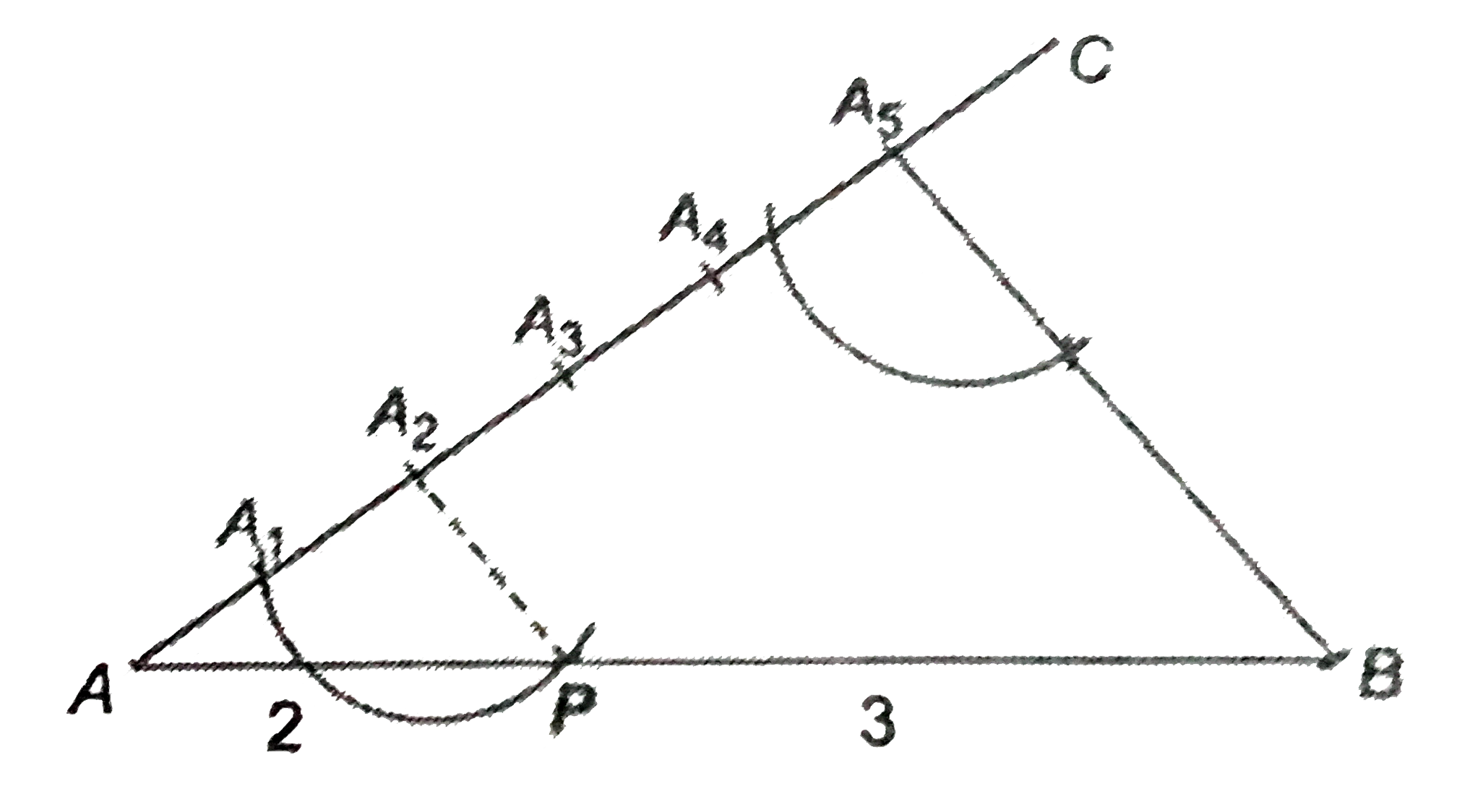
4. Join BA5
5. Through A2 draw a line A2P parallel to A5B by making an angle equal to ∠∀5B at A2 intersecting AB at a point P.
The point P so obtained is the required point.
Justification: In ΔAA5B,
A2P∣∣A5B ( construction )
∴AA2A2A5=APPB (by. B.P. theorem)
⇒23=APPB(construction )
⇒AP:PB=2:3
i.e., P divides AB internally in the ratio 2:3.
Alternate Method:
We can use one more method for this question.
1. Draw the line segment AB=7 cm
2.Draw any ray AC making an acute angle ∠BAC with AB.
3. Draw a ray BD parallel to AC by making ∠ABC equal to angle ∠BAC.
4. Mark off 2 points A1 and A2 on AC and 3 points B1,B2,B3 on AD such that
AA1=A1A2=BB1=B1B2=B2B3
5. Join B3A2, suppose it intersect AB at point P. Then, P is the require point.

Topper's Solved these Questions
- CONSTRUCTIONSBOOK - NAGEEN PRAKASHANCHAPTER - CONSTRUCTIONSEXERCISE - Construction of Tangents to a Circle
5 Videos
- CONSTRUCTIONSBOOK - NAGEEN PRAKASHANCHAPTER - CONSTRUCTIONSEXERCISE - PROBLEMS FROM NCERT/ EXEMPLAR
10 Videos
- CO-ORDINATE GEOMETRYBOOK - NAGEEN PRAKASHANCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - Revision Exercise Short Answer Questions
9 Videos
- INTRODUCTION TO TRIGONOMETRYBOOK - NAGEEN PRAKASHANCHAPTER - INTRODUCTION TO TRIGONOMETRYEXERCISE - Revision Exercise Long Answer Questions
5 Videos
Similar Questions
Determine a point which divides a line segment 6cm long externally in the ratio 5:3
View SolutionDetermine a point which divides a line segment 6 cm long externally in the ratio 3:5.
View SolutionDetermine a point which divides a line segment 6cm long externally in the ratio 5:3
View SolutionDetermine a point which divides a line segment 6 cm long externally in the ratio 3:5.
View SolutionDivide a line segment of length 10cm internally in the ratio 3:2
View SolutionDivide a line segment of length 8cm internally in the ratio 3:4 .
View SolutionDivide a line segment of length 8 cm internally in the ratio 4:2 .
View SolutionDivide a line segment of length 10 cm internally in the ratio 5:4.
View SolutionFind the coordinates of the point which divides the line segment joining (−1, 3) and (4, −7) internally in the ratio 3:4 .
View SolutionFind the coordinates of the point which divides the line segment joining (−1, 3) and (4, −7) internally in the ratio 3:4 .
View Solution
