Question

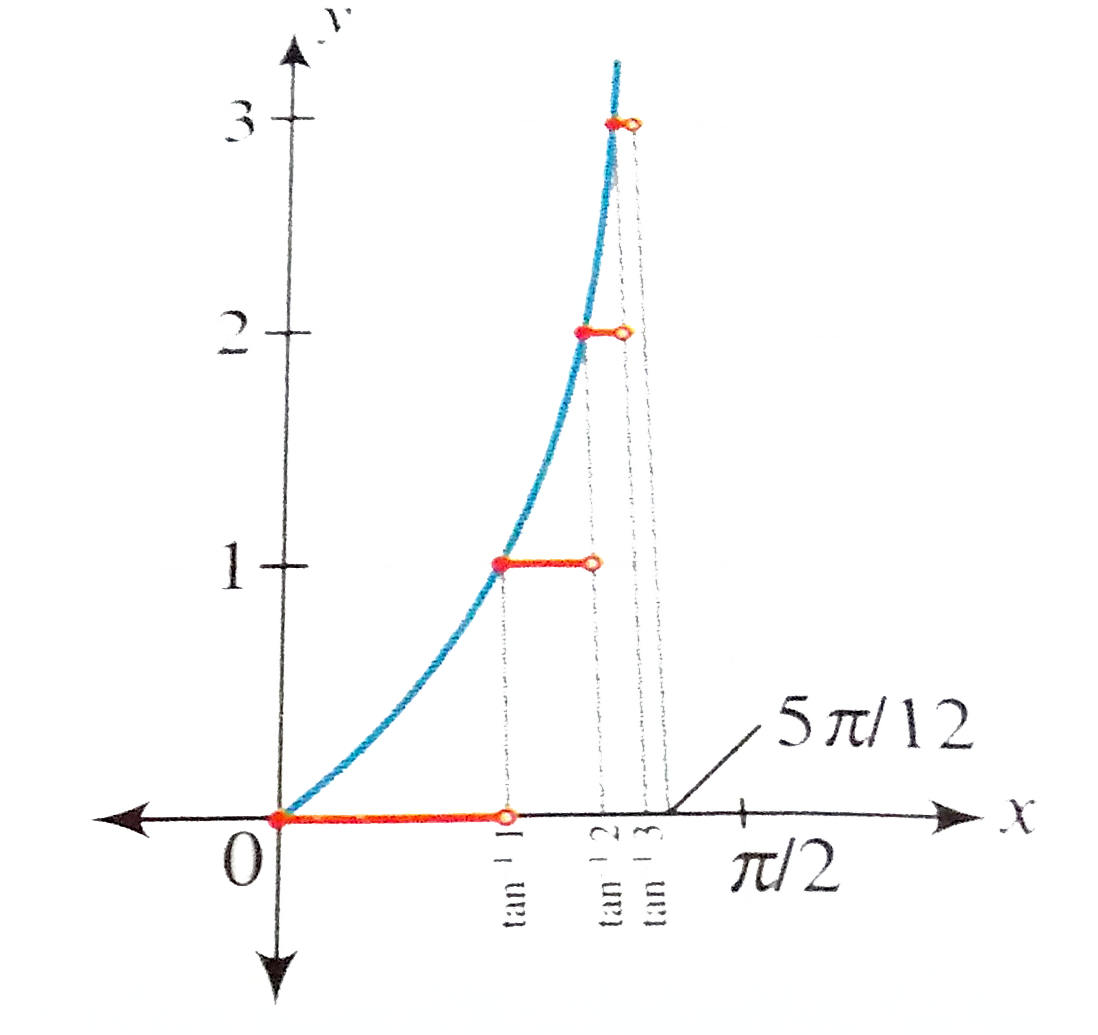
Draw the graph of $f\left(x\right)=\left[\tan x\right],0\le x\le 5\pi /12$, where $[\cdot ]$ represents the greatest integer function.

Explanation

`f(x) = [tan x]`
tan x is an increasing function in `[0, 5pi//12]`
tan 0 = 0 and `tan (5pi//12) = 2 + sqrt(3)`
Now [tan x] is discontinuous when tan x is an integer.
So f(x) is discontinuous when `tan x = 1, 2, 3 (lt 2 + sqrt(3))`
`therefore ` `x = tan^(-1) 1, tan^(-1) 2, tan^(-1) 3`
`f(x) = [tan x] = {{:(0", " tan x in [0", "1) or x in [0"," tan^(-1)1)),(1", " tan x in [1", " 2) or x in [tan^(-1)1"," tan^(-1)2)),(2", " tan x in [2", " 3) or x in [tan^(-1)2, tan^(-1)3)),(3", " tan x in [3", " 2 + sqrt(3)) or x in [tan^(-1)3, 5pi//12)):}`
So the graph of the function is as shown in the following figure.