Question

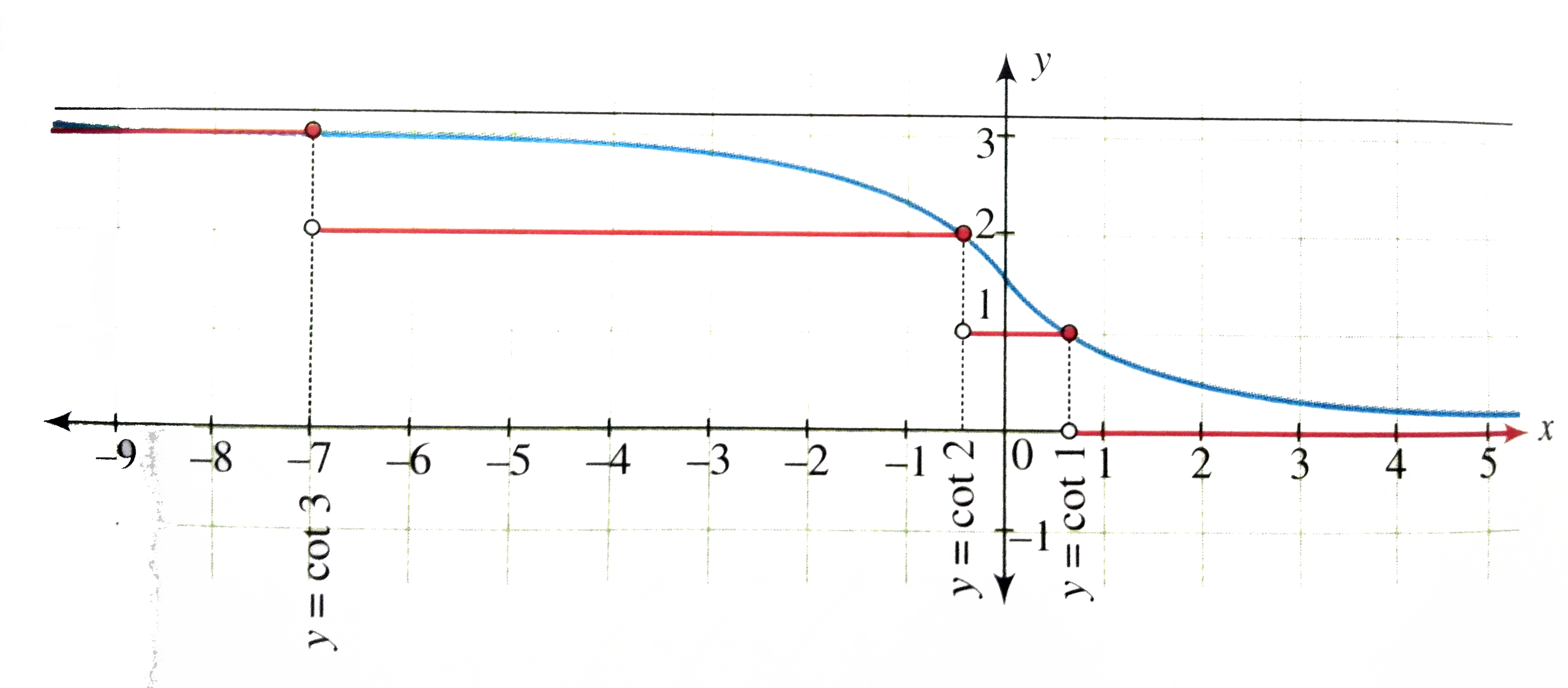
Draw the graph of $f\left(x\right)=\left[{\cot }^{-1}x\right],\text{where}[\cdot ]$ represents the greatest integer funtion.

Explanation

Given `f(x)=[cos^(-1)x]`
`cot^(-1)x` is a decreasing function in R.
So `[cot^(-1)x]` is discontinuous whn `cot^(-1)x` is an interger.
Now `0lecot^(-1)x lepi" for "x in R`
So `[cot^(-1)x]` is discontinuous when`cot^(-1)x=1,2,3`
or `x=cot1, cot2, cot3`
When `[cot^(-1)x]=0,0lecot^(-1)xlt1:.cot1ltxleoo`
When `[cot^(-1)x]=1,1lecot^(-1)xlt2:.cot2ltxlecot1` ltbrtgt When `[cot^(-1)x]=2,2lecot^(-1)xlt3:.cot3ltxlecot2`
`[cot^(-1)x]=3,3lecot^(-1)xltpi:.-ooltxlecot3`
So the graph of `f(x)[cot^(-1)x]` can be drawn as follows.