Draw the graph of the function f(x)=x−∣∣x−x2∣∣,−1≤x≤1 and find the points of non-differentiability.

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

We have y=f(x)=x−∣∣x−x2∣∣
={x−(x2−x),x2−x≥0x−(x−x2),x2−x<0
={x−(2x−x2),x≤0orx≥1x2,0<x<1
The graph of the function y=2x−x2=x(2−x) is a downward parabola intersecting the x-axis at x=0andx=2.
Thus, the graph of the function y=f(x) is as follows:
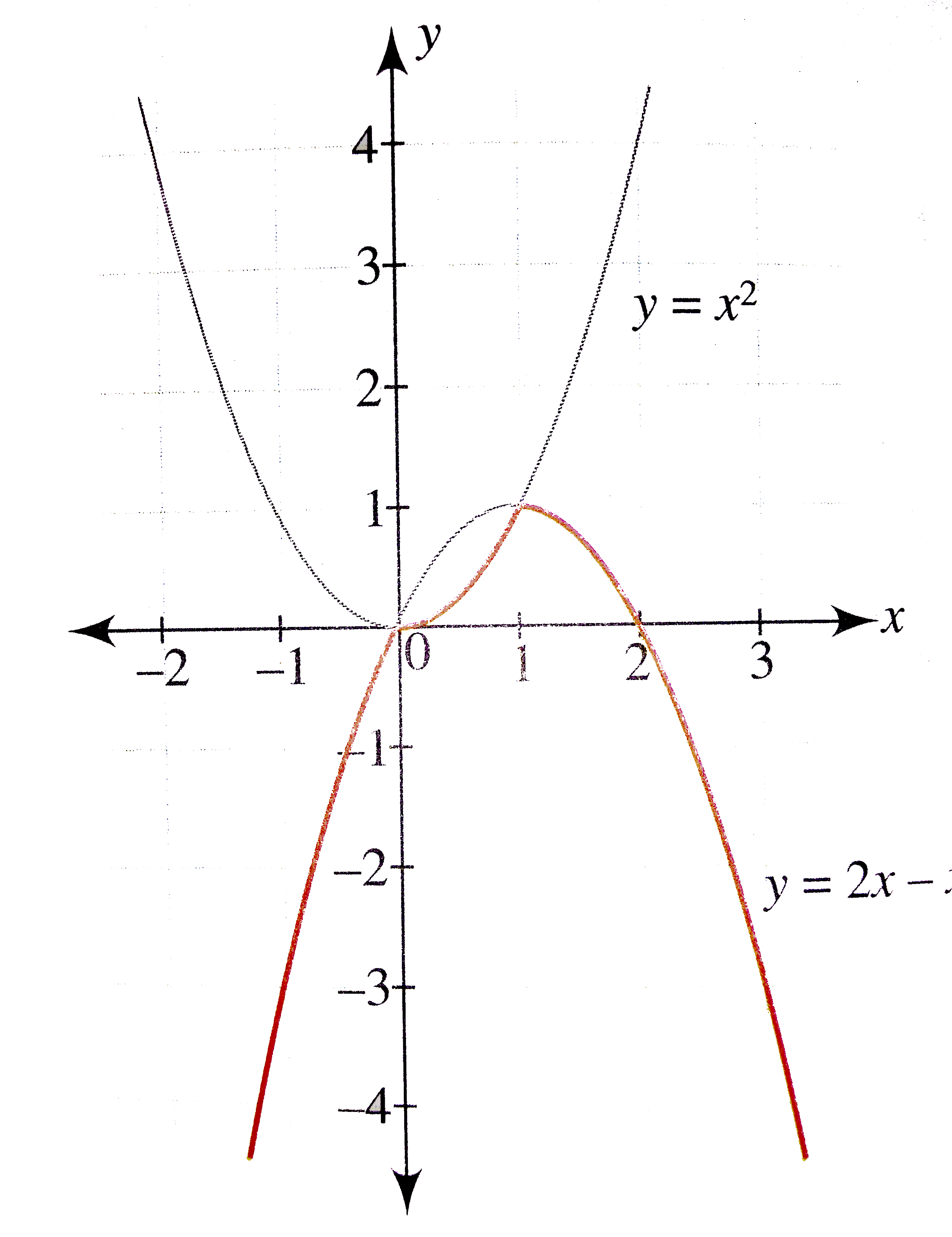
ocr_image
Clearly from the graph the function is continuous but non-differentiable at x=0,1.

Updated on:21/07/2023
|
Class 12MATHSFUNDAMENTAL OF MATHEMATICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • If function f(x)=x−∣∣x−x2∣∣,−1≤x≤1 then f is

    Acontinous at x=0
    Bcontinous at x=1
    Ccontinous at x=-1
    Deverywhere continous

  • The range of the function f(x)=|x−1|+|x−2|,−1≤x≤3, is

    A[1, 3]
    B[1, 5]
    C[3, 5]
    DNone of these

  • The function f(x)=x−∣∣x−x2∣∣,−1≤x≤1 is continuous on the interval

    A[−1,1]
    B(−1,1)
    C{−1,1]−{0}
    D(−1,1)−{0}