Draw the graph of y=sin−1|sinx|andy=(sin−1|sinx|)2,0≤x≤2π
Text Solution
We have y=f(x)=sin−1|sinx|,0≤x≤2π
{sin−1(sinx)0≤x<π−sin−1(sinx)π≤x≤2π
{x0≤x<π2π−xπ2≤x<π
⎧⎪
⎪
⎪
⎪
⎪
⎪
⎪⎨⎪
⎪
⎪
⎪
⎪
⎪
⎪⎩x0≤x<π2π−xπ2≤x<p−(π−x)π≤x<3π2−(x−2π)2π23π2≤x<2π
⎧⎪
⎪
⎪
⎪
⎪
⎪
⎪⎨⎪
⎪
⎪
⎪
⎪
⎪
⎪⎩x0≤x<π2π−xπ2≤x<p−(π−x)π≤x<3π2x−2π3π2≤x<2π
The graph of y=f(x) is as shown in the following figure.
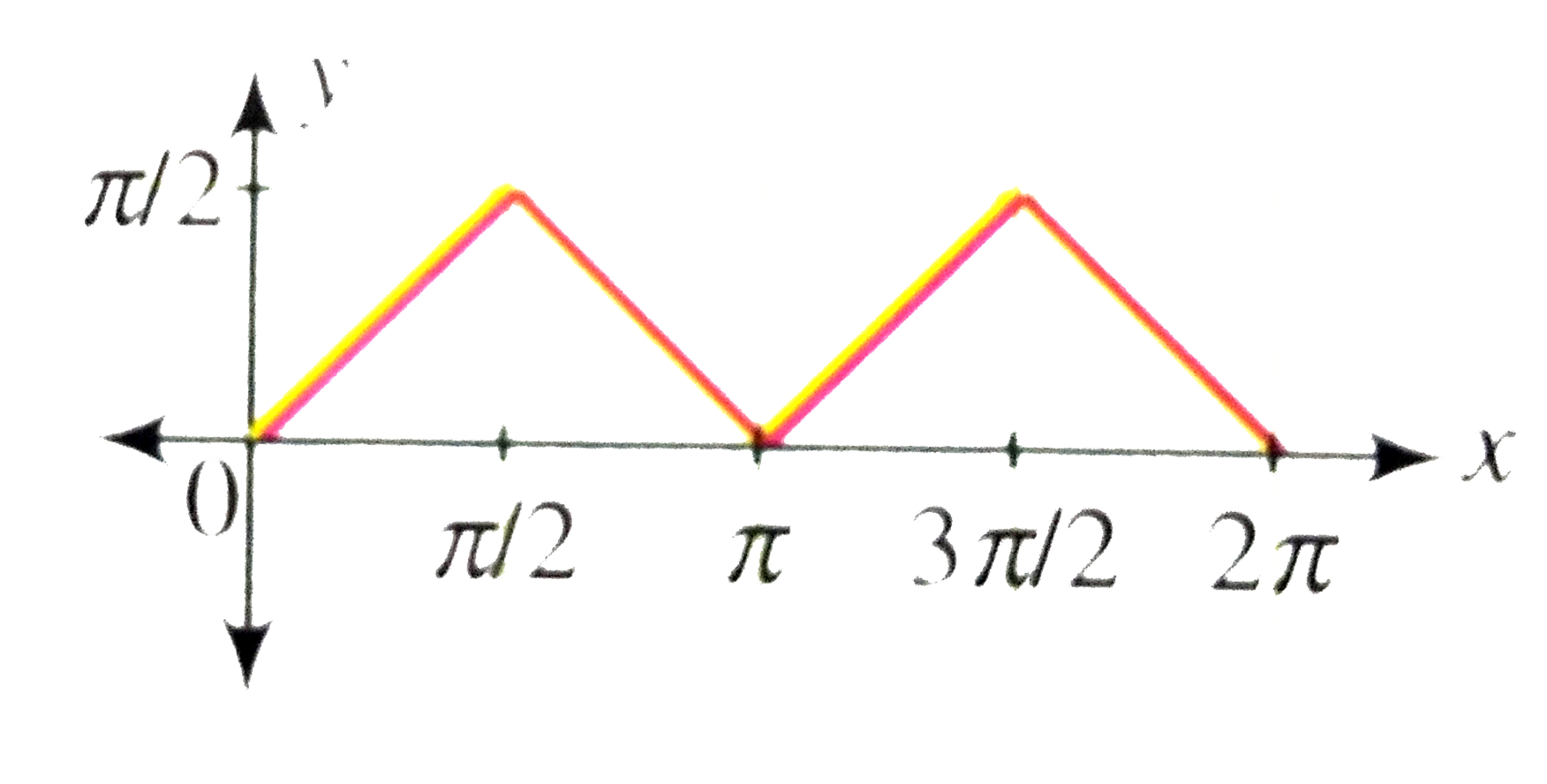
y=g(x)=(sin−1|sinx|)2,0≤x≤2π
⎧⎪
⎪
⎪⎨⎪
⎪
⎪⎩x20≤x<π2(π−x)2π2≤x<π(x−π)2π≤x<3π2=⎧⎪
⎪
⎪⎨⎪
⎪
⎪⎩x20≤x<π2(π−x)2π2≤x<π(2π−x)22π2≤x<2π
y=x2 is parabola having vertex at (0,0)
y=(x−π)2 is a parabola having vertex at (π,0)
y=(x−2π)2is a parabola having vertex at (2π,0)
The graph of y=g(x) is as shown in the followin figure.
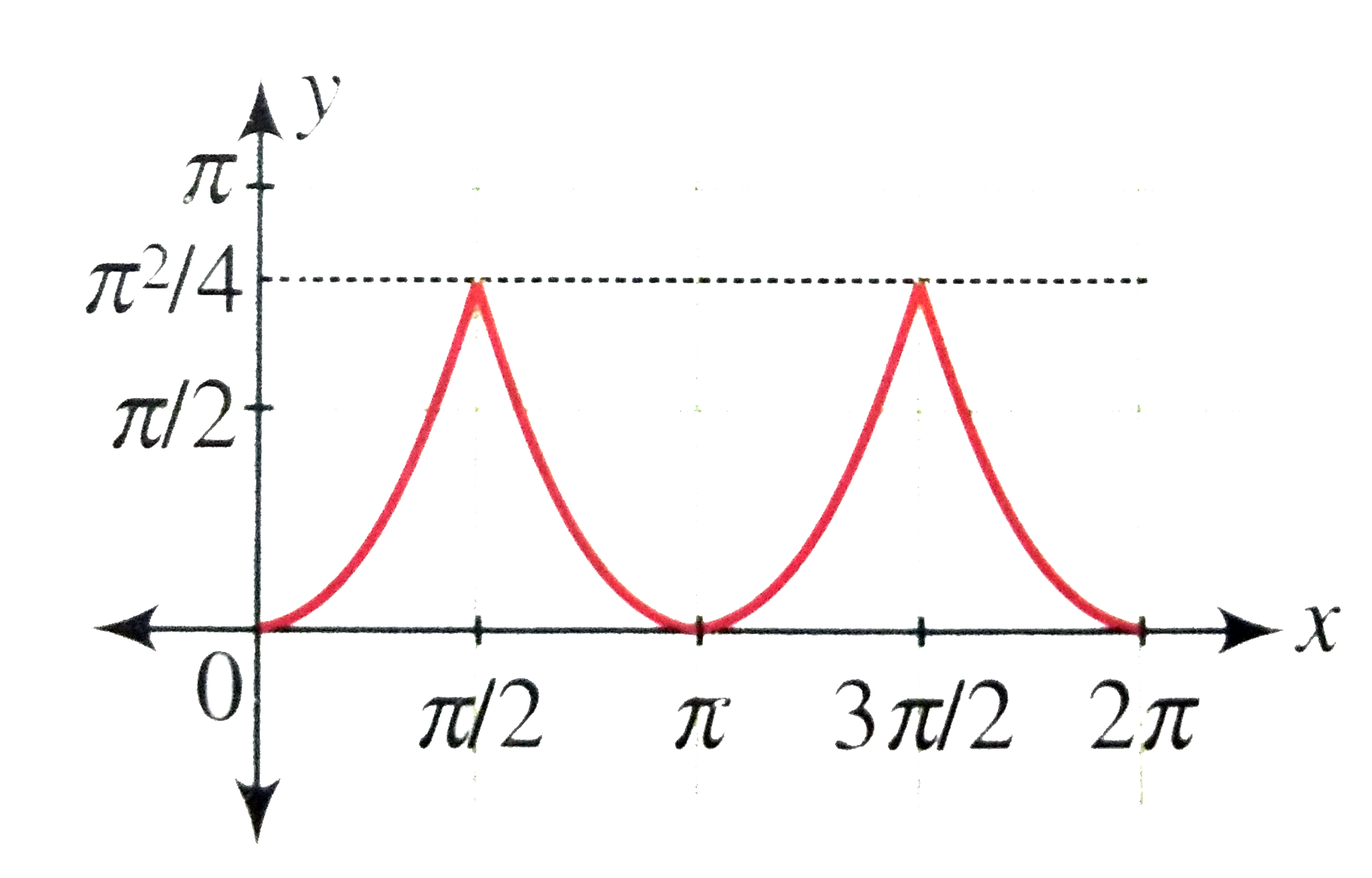
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise18videos
GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGECHAPTER - GETTING STARTED WITH GRAPHSEXERCISE - Exercise18videos
GETTING STARTED WITH GRAPHS
- BOOK - CENGAGECHAPTER - GRAPHICAL TRANSFORMATIONSEXERCISE - Exercise22videos
GRAPHICAL TRANSFORMATIONS
Similar Questions
Draw the graph of y=sin−1(sinx)
View SolutionDraw the graph of y=sin−1(sinx)
View SolutionDraw the graph of y=sin−1|x|.
View SolutionDraw the graph of y=sin−1|x|.
View SolutionDraw the graph of y=sin−1(x2)
View SolutionDraw the graph of y=sin−1(x2)
View SolutionDraw the graph of y=sin−1(x−3).
View SolutionDraw the graph of y=sin−1(x−3).
View SolutionDraw the graph of y=sin2x.
View SolutionDraw the graph of y=sin2x−cosx
View Solution
