Equation of the smaller circle that touches the circle x2+y2=1 and passes through the point (4,3) is
Video Solution
Text Solution
Required circle through proint A(4,3) touches the circle S1≡x2+y2=1.
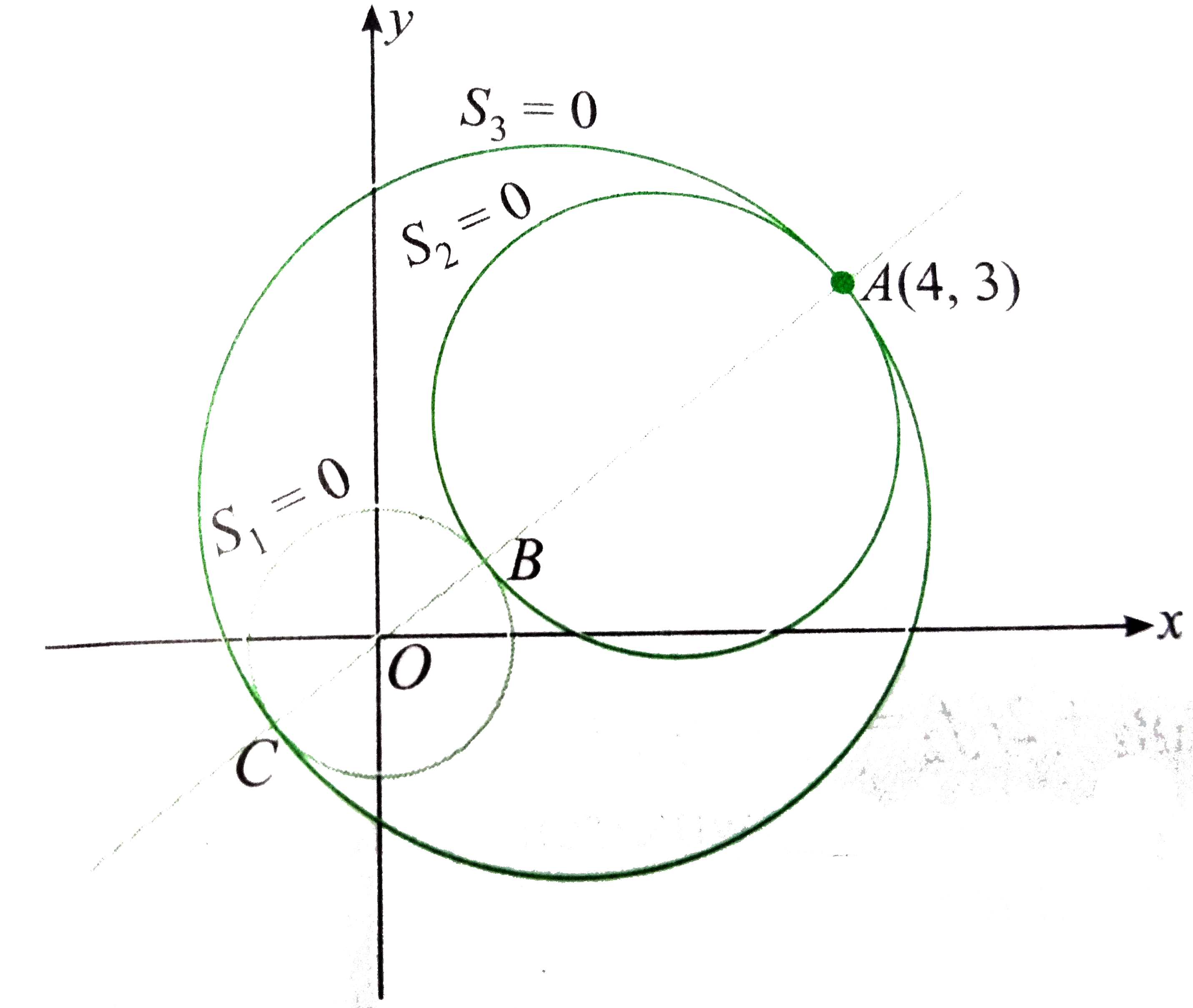
This circle is smallest if it touches the given circle externally and point of contact B lies on the common normal.
Equation of line OA is y=34x (1)
Putting this value of y from (1) in x2+y2=1 , we get
x=±(4)?(5) and y=±35
∴B=(45,35)
and C=(−45,−35)
Therefore, equation of circle with AB as diameter is
S2≡(x−45)(x−4)+(y−3)(y−35)=0
or x2+y2−245x−185y=0
Required circle is the largenst if given circle touches given circle internally and point of contact C lies on the common normal.
Therefore, equation of circle with AC as diameter is
S3=(x+45)(x−4)+(y+35)(y−3)=0
or x2+y2−165x−125y−5=0
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
Equation of a circle with centre (4,3) touching the circle x2+y2=1 is
Ax2+y2−8x−6y−9=0Bx2+y2−8x−6y+11=0Cx2+y2−8x−6y−11=0Dx2+y2−8x−6y+9=0The length of the radius of the circle which touches the x - axis at the point (1, 0) and passes through the point (2, 3) is
A103 unitsB35 unitsC65 unitsD53 unitsEquation of the circle touching the circle x2+y2−15x+5y=0 at ( 1,2) and also passing through the point (0,2) is :
Ax2+y2−x−2y=0Bx2+y2+2x=0C13(x2+y2)−13x−61y+70=0Dnone of these
Find the equation of the circle concentric with the circle x2+y2−4x−6y−9=0 and passing through the point (−4,−5)
View SolutionFind the equation of the circle which touches the axis of x and passes through the two points (1,-2) and (3,-4)
View SolutionEquation of a circle with centre(4,3) touching the circle x2+y2=1
View SolutionThe length of the diameter of the circle which touches the x-axis at the point (1, 0) and passes through the point (2, 3)
View SolutionThe radius of the circle, which touches the parabola y2=4x at (1,2) and passes through the origin is:
View Solution
