Find tha area of the region containing the points (x,y) satisfying 4≤x2+y2≤2(|x|+|y|). Solution in Tamil
8 sq. units
2 sq. units
4π sq. units
2π sq. units
The correct Answer is:A
The points in the required region satisfy
4≤x2+y2≤2(|x|+|y|) …(1)
Since the curve (1) is symmetrical about both the axes, the required area is 4 times the area of the region in the first quadrant. Therefore, it is sufficient to sketch the region and to find the area in the first quadrant.
In the first quadrant, the curve (1) consist of two curves
x2+y2≥4 (C1)
and x2+y2−2x−2y≥0 (C2)
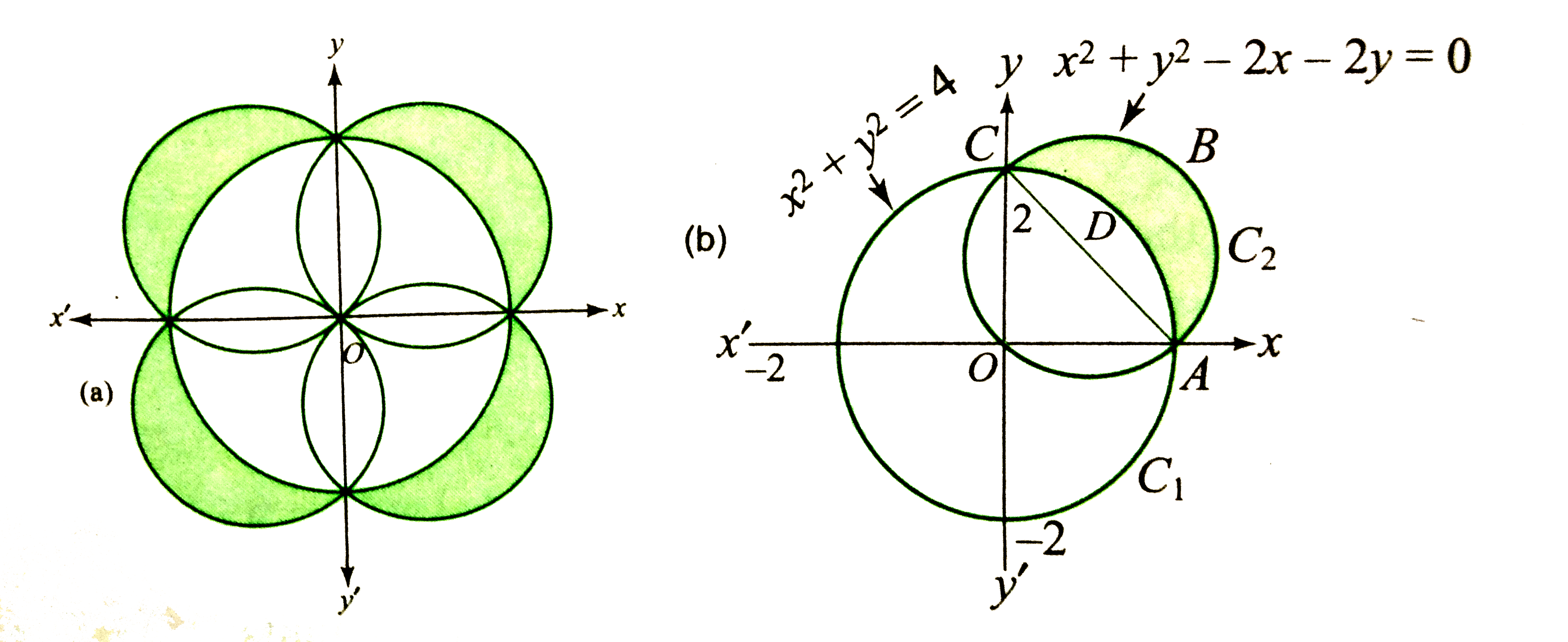
∴ Required area =4 (area ABCDA)
=4(area of semi-cirlce ABCA)-(area of sector ADCBA)
=4(area of semi-circle ABCA)-(area of sector OADCO-area of triangle OAC)
=4{π−(π−2}=8 sq. units.
Topper's Solved these Questions
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise (Multiple)
10 Videos
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise (Comprehension)
21 Videos
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise 9.3
7 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGECHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Subjective Type
2 Videos
- AREA UNDER CURVESBOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank
10 Videos
Similar Questions
Let A(k) be the area bounded by the curves y=x2−3 and y=kx+2 The range of A(k) is (10√53,∞) The range of A(k) is (20√53,∞) If function k→A(k) is defined for k∈[−2,∞ ), then A(k) is many-one function. The value of k for which area is minimum is 1.
View SolutionLet Ar be the area of the region bounded between the curves y2=(e−kr)x(where k>0,r∈N) and the line y=mx(where m≠0), k and m are some constants
A1,A2,A3,… are in G.P. with common ratio
View SolutionFind the continuous function f where (x4−4x2)≤f(x)≤(2x2−x3) such that the area bounded by y=f(x),y=x4−4x2. then y-axis, and the line x=t, where (0≤t≤2) is k times the area bounded by y=f(x),y=2x2−x3,y−aξs, and line x=t(where0≤t≤2).
View SolutionProve that for λ>1, the equation xlogx+x=λ has least one solution in [1,λ].
View SolutionThe area of the region (s) enclosed by the curves y=x2 and y=√|x| is
View SolutionFind tha area of the region containing the points (x,y) satisfying 4≤x2+y2≤2(|x|+|y|).
View SolutionFind the area of the region formed by the points satisfying
|x|+|y|+|x+y|≤2.
View SolutionThe area (in sq units) of the region
A={(x,y):y22≤x≤y+4} is
View SolutionFind the area of the region [x,y):x2+y2≤1≤x+y}
View SolutionFind the area of the region {(x,y):x2+y2≤2ax , y2≤ax , x≤0 , y≤0}
View SolutionThe area of the region bounded by the curves {(x,y):x2+y2≤4,2≤x+y} is __________ .
View Solutionक्षेत्र {(x,y):0≤y≤x2+1,y≤x+1,0≤x≤2} का क्षेत्रफल ज्ञात कीजिए।
View SolutionFind tha area of the region containing the points (x,y) satisfying 4≤x2+y2≤2(|x|+|y|).
View SolutionFind the area of the region formed by the points satisfying
|x|+|y|+|x+y|≤2.
View SolutionFind the area bounded by the region given by : A={(x,y):x29+y24≤1≤x3+y2}.
View SolutionThe area of the region described by A = {(x,y) : x^(2)+y^(2) le 1 and y^(2) le 1-x} is :
View Solution
