Find the area of the region bounded by the ellipse $\frac{x^{2}}{16} + \frac{y^{2}}{9} = 1$ .

Video Solution

Text Solution

Verified by Experts

Given curve is an ellipse which is symmetric about X-axis both, as shown in the figure.

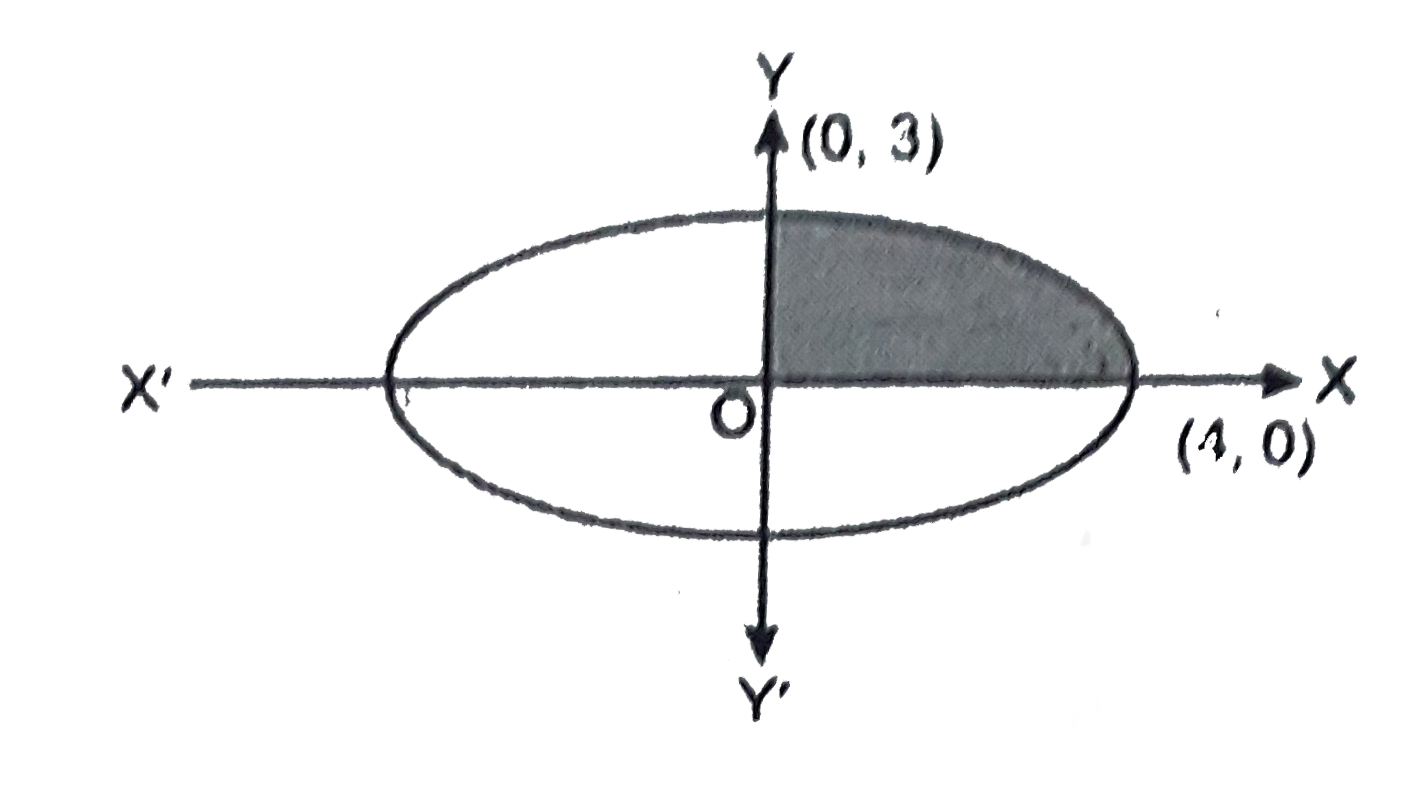
$∴$ Area bounded by ellipse
$= 4 \times$ (area of shaded region in first quadrant)
$= 4 \times \int_{0}^{4} y d x$
$= 4 \int_{0}^{4} \frac{3}{4} \sqrt{16 - x^{2}} d x$
$= 3 \cdot \int_{0}^{4} \sqrt{4^{2} - x^{2}} d x$
$= 3 {[\frac{x}{2} \sqrt{4^{2} - x^{2}} + \frac{4^{2}}{2} {sin}^{- 1} (\frac{x}{4})]}_{0}^{4}$
$= 3 [2 \sqrt{16 - 16} + 8 {sin}^{- 1} (1) - 0 - 8 \sin^{- 1} (0)]$
$= 3 [0 + 8 {sin}^{- 1} (1) - 0]$
$= 3 \times 8 \times (\frac{π}{2}) = 12 π$ sq. units.

Find the area of the region bounded by the ellipse $\frac{x^{2}}{9} + \frac{y^{2}}{4} = 1$ in fourth quadrant.
A $\frac{3 π}{4}$ sq unit
B $\frac{3 π}{2}$ sq unit
C $\frac{9 π}{4}$ sq unit
D $\frac{4 π}{7}$ sq unit
Find the area of the region bounded by the ellipse $\frac{x^{2}}{4} + \frac{y^{2}}{9} = 1 .$

A $10 π$
B $11 π$
C $12 π$
D $13 π$
Find the area of the region bounded by the ellipse $\frac{x^{2}}{9} + \frac{y^{2}}{4} = 1$ in fourth quadrant.
A $\frac{3 π}{4}$ sq units
B $\frac{3 π}{2}$ sq units
C $\frac{5 π}{2}$ sq units
DNone of these