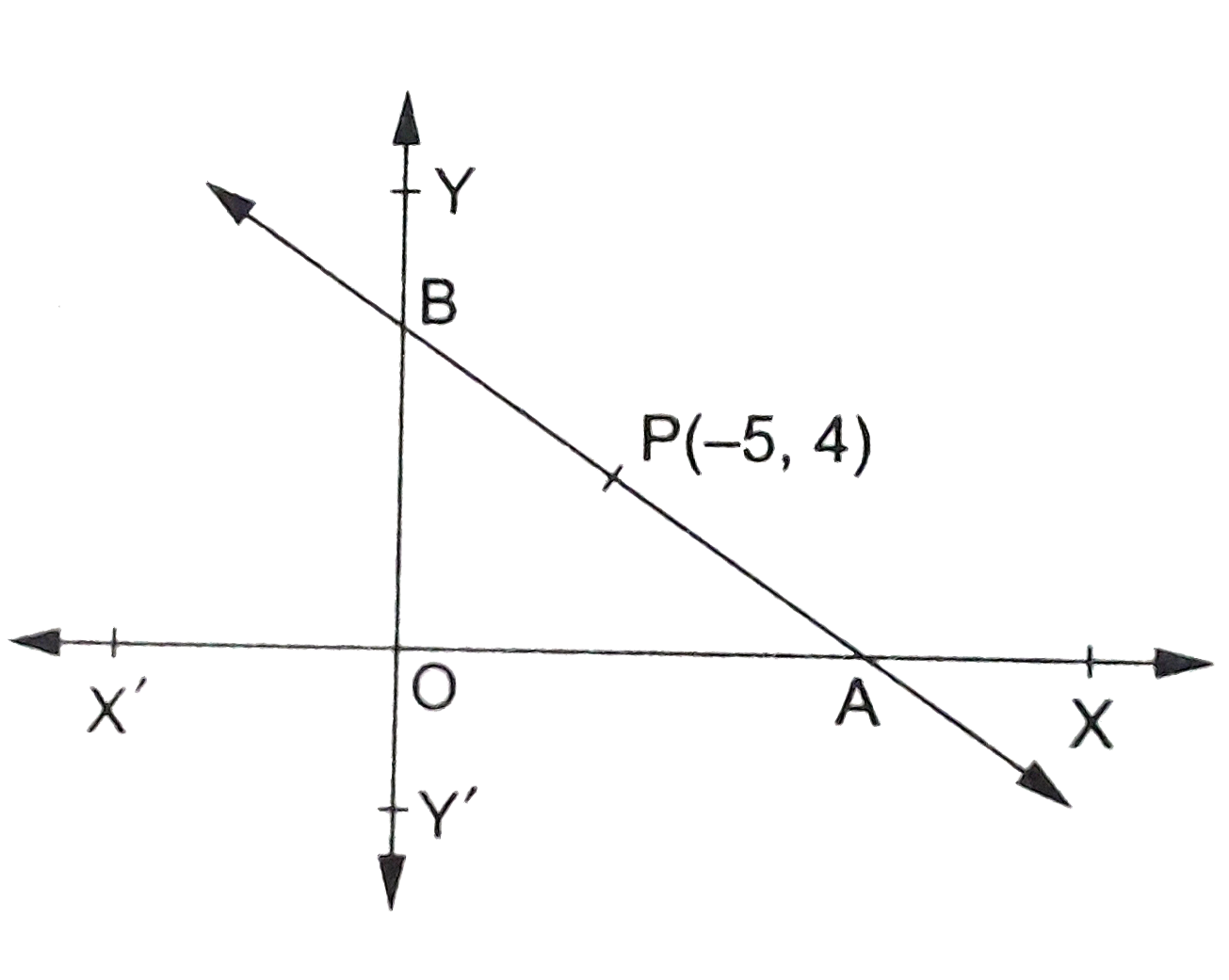
Find the equation of the line so that the segment intercept between the axes is divided by the point P(5,-4) in the ratio 1:2

Video Solution

Text Solution

Verified by Experts

Let AB be the given the line segment making intercept a and b on the x-axis and y-axis respectively. Then the equation of line AB is $\frac{x}{a} + \frac{y}{b} = 1$
So, these points are A(a,0) and B(0,b) Now, P(-5,4) divides AB in the ration 1:2
$∴ \frac{(1 \times 0 + 2 \times a)}{(1 + 2)} = - 5 and \frac{(1 \times b + 2 \times 0)}{(1 + 2)} = 4 \Leftrightarrow a = \frac{- 15}{2}, and b = 12$
So, hte required equation of the line is $\frac{x}{(\frac{- 15}{2})} + \frac{y}{12} = 1 \Leftrightarrow \frac{- 2 x}{15} + \frac{y}{12} = 1$
$\Leftrightarrow 8 x - 5 y + 60 = 0$
Hence, the required equation of the line is $8 x - 5 y + 60 = 0$ .

Updated on:21/07/2023