Find the equations of the circles passing through the point (−4,3) and touching the lines x+y=2 and x−y=2
Since circles touch the lines x+y=2 and x−y=2, centre lies on x-acis or y-axis.
But circle passes through the point Q(−4,3). So, centre lies on negative x-axis.
Let the centre be C(h,0).
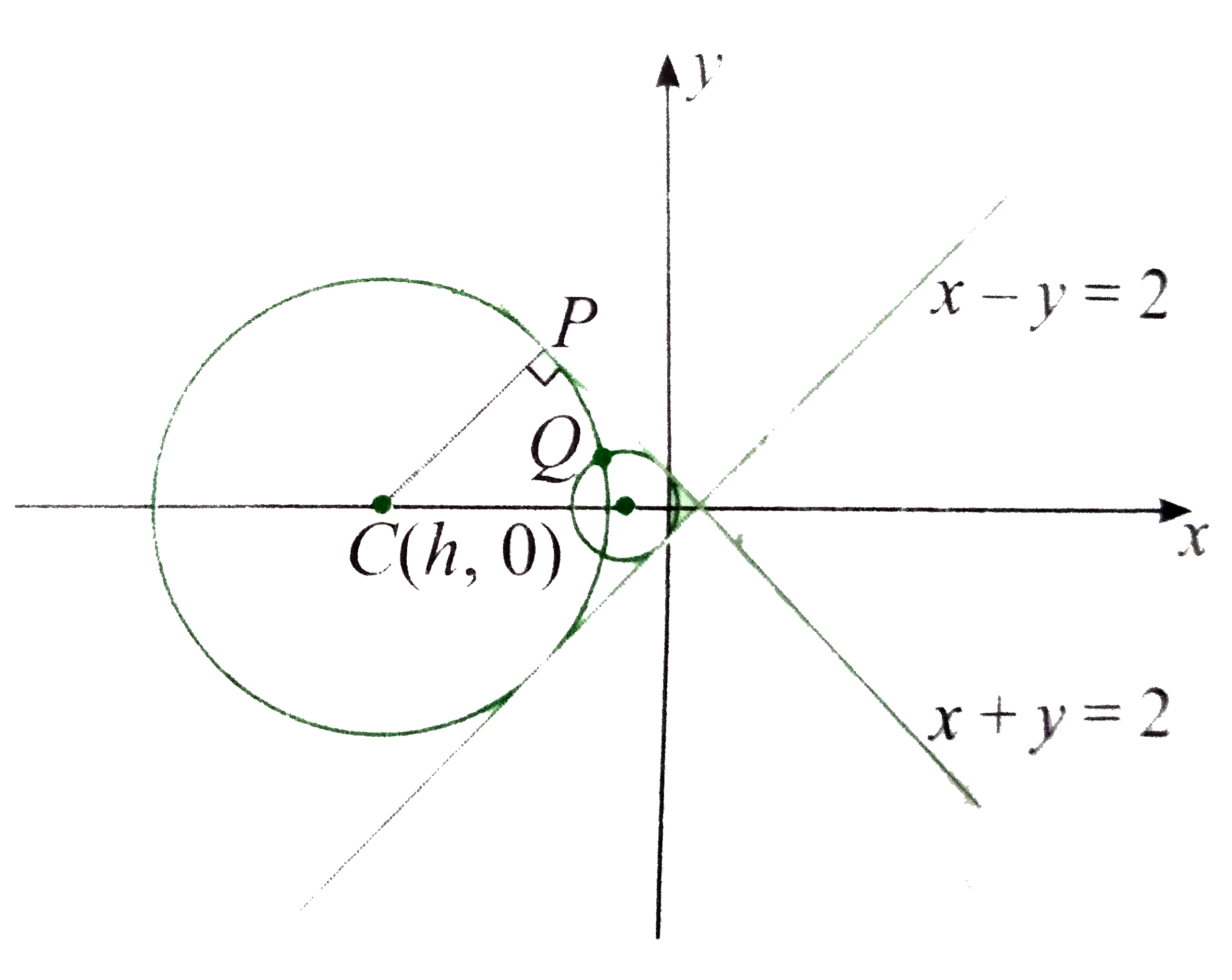
Also, radius, CP= distance of centre from the line x−y=0 ( or x+y−2=0)
=|h−0−2|√12+(−1)2=|h−2|√2
Also, radius, CQ=√(h+4)2+(k−3)2
∴CQ=CP
⇒(h−2)22=(h+4)2+(0−3)2
⇒h=−20±√202−4(46)2
⇒h=−10±3√6
Thus, equation of the circle is (x−h)2+y2=(h−2)22, where h=−10±3√6
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One or More
An equation of a line passing through the point (−2,11) and touching the circle x2+y2=25 is
A4x+3y=25B3x+4y=38C24x−7y+125=0D7x+24y−230=0
Find the equation of the circle passing through the point (1,9), and touching the line 3x+4y+6=0 at the point (-2,0) .
View SolutionFind the equation of the line passing through the point (2,-5) and parallel to the line 2x-3y=7.
View SolutionFind the equation of circle passing through the points (1,-2) and (3,-4) and touches the X-axis.
View SolutionFind the gradient of the line passing through the point (2,8) and touching the curve y=x3.
View SolutionFind the equation of the line passing through the point (2, 3) and perpendicular to the line 4x+3y=10.
View SolutionFind the equation of the circle passes through the points (2,1) and (−2,3) and has centre on the line x+y+4=0
View SolutionFind the equation of the circle passing through the point (−1,3) and having its centre at the point of intersection of the lines x−2y=4 and 2x+5y+1=0
View Solution

