Find the locus of the midpoint of the chords of the circle $x^{2} + y^{2} = a^{2}$ which subtend a right angle at the point $(c, 0) .$

Video Solution

Text Solution

Verified by Experts

Let P(h,k) be the midpoint of a chord AB of the circle which subtends a right angle at C(c,0).

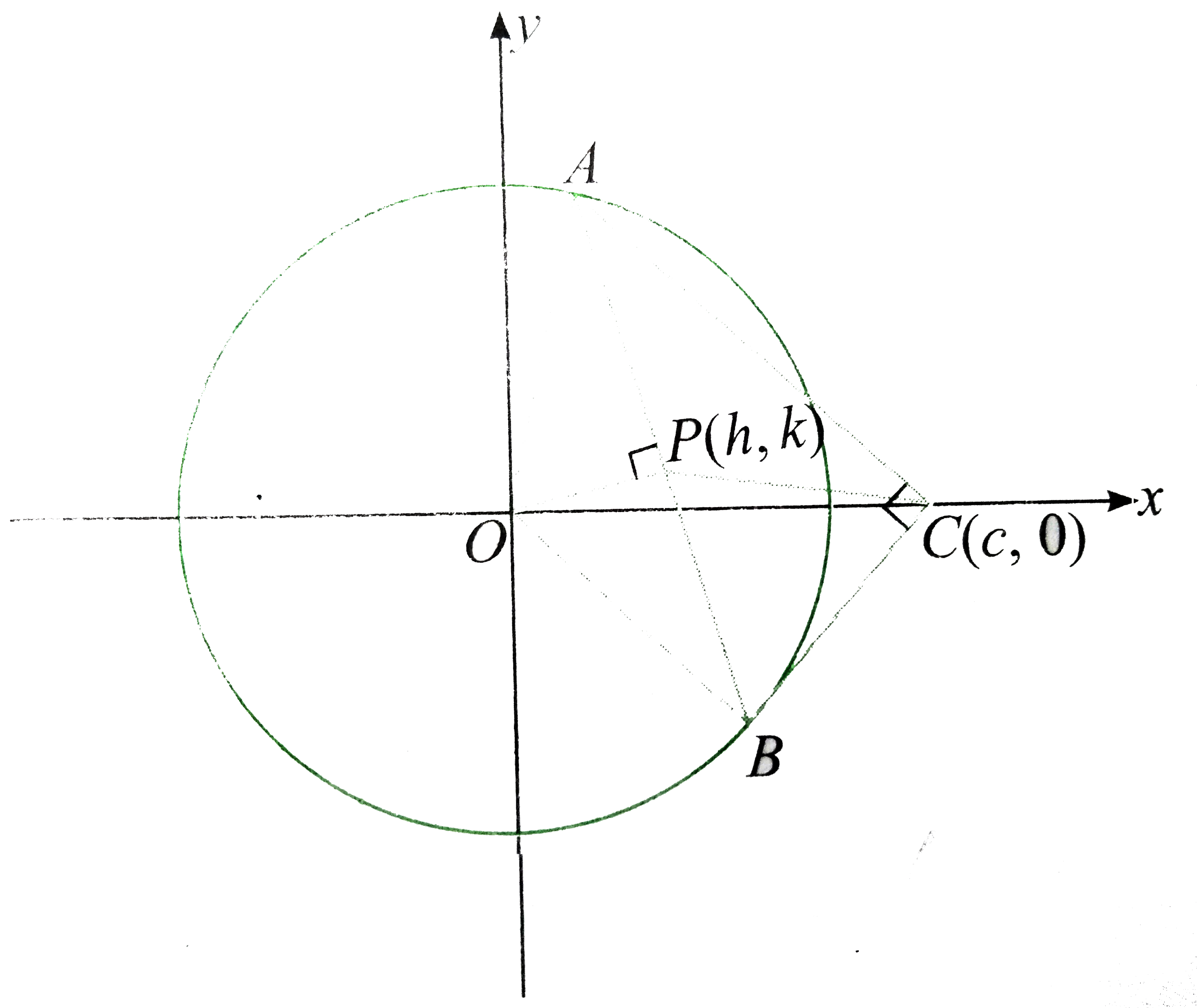
In right angles triangle ACB, we have
$P A = P C = P B$
$P C = \sqrt{{(h - c)}^{2} + k^{2}}$
$P B = P A = \sqrt{O A^{2} - O P^{2}}$
$= \sqrt{a^{2} - (h^{2} + k^{2})}$
Now , $P C = P A$
$∴ \sqrt{{(h - c)}^{2} + k^{2}} = \sqrt{a^{2} - (h^{2} + k^{2})}$
$\Rightarrow {(h - c)}^{2} + k^{2} = a^{2} - (h^{2} + k^{2})$
Therefore , the equation of required locus is $2 (x^{2} + y^{2}) - 2 c x + c^{2} - a^{2} = 0$

Updated on:21/07/2023