Find the polar coordinates of the points whose cartesian coordinates are
(−3,4)
The correct Answer is:(5,π−tan−1(43))
To find the polar coordinates of the point with Cartesian coordinates (-3, 4), we will follow these steps:
Step 1: Identify the Cartesian Coordinates
The given Cartesian coordinates are:
- x=−3
- y=4
Step 2: Calculate the Radius r
The formula for calculating the radius r in polar coordinates is:
r=√x2+y2
Substituting the values of x and y:
r=√(−3)2+(4)2=√9+16=√25=5
Step 3: Calculate the Angle θ
The angle θ can be found using the tangent function:
tan(θ)=yx
Substituting the values of y and x:
tan(θ)=4−3
This gives us:
θ=tan−1(4−3)
Since the point (-3, 4) is located in the second quadrant (where x<0 and y>0), we need to adjust the angle:
θ=π+tan−1(4−3)
To find the angle in the second quadrant, we can also express it as:
θ=π−tan−1(43)
Step 4: Final Polar Coordinates
Now we can express the polar coordinates as:
(r,θ)=(5,π−tan−1(43))
Conclusion
The polar coordinates of the point whose Cartesian coordinates are (-3, 4) are:
(5,π−tan−1(43))
---
The given Cartesian coordinates are:
- x=−3
- y=4
The formula for calculating the radius r in polar coordinates is:
r=√x2+y2
Substituting the values of x and y:
r=√(−3)2+(4)2=√9+16=√25=5
The angle θ can be found using the tangent function:
tan(θ)=yx
Substituting the values of y and x:
tan(θ)=4−3
This gives us:
θ=tan−1(4−3)
Since the point (-3, 4) is located in the second quadrant (where x<0 and y>0), we need to adjust the angle:
θ=π+tan−1(4−3)
To find the angle in the second quadrant, we can also express it as:
θ=π−tan−1(43)
Now we can express the polar coordinates as:
(r,θ)=(5,π−tan−1(43))
The polar coordinates of the point whose Cartesian coordinates are (-3, 4) are:
(5,π−tan−1(43))
Topper's Solved these Questions
- COORDINATE SYSTEM AND COORDINATES BOOK - ARIHANT MATHS ENGLISHCHAPTER - COORDINATE SYSTEM AND COORDINATES EXERCISE - Exercise For Session 1
10 Videos
- COORDINATE SYSTEM AND COORDINATES BOOK - ARIHANT MATHS ENGLISHCHAPTER - COORDINATE SYSTEM AND COORDINATES EXERCISE - Exercise For Session 2
19 Videos
- CONTINUITY AND DIFFERENTIABILITYBOOK - ARIHANT MATHS ENGLISHCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
20 Videos
- DEFINITE INTEGRALBOOK - ARIHANT MATHS ENGLISHCHAPTER - DEFINITE INTEGRALEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
38 Videos
Similar Questions
Find the polar coordinates of the points whose cartesian coordinates are
(−2,−2)
View SolutionThe polar coordinates of the point whose cartesian coordinates are (-1, -1) is
View SolutionFind the cartesian coordinates of the points whose polar coordinates are
(5,π−tan−1(43))
View SolutionFind the Cartesian co-ordinates of point whose polar co-ordinates are (4,π3).
View SolutionThe cartesian coordinates of the point whose polar coordinates are (13,π−tan−1(512)) is
View SolutionConvert the polar coordinates to its equivalent Cartesian coordinates(2,π).
View SolutionIn Fig 4 the coordinates of point D are
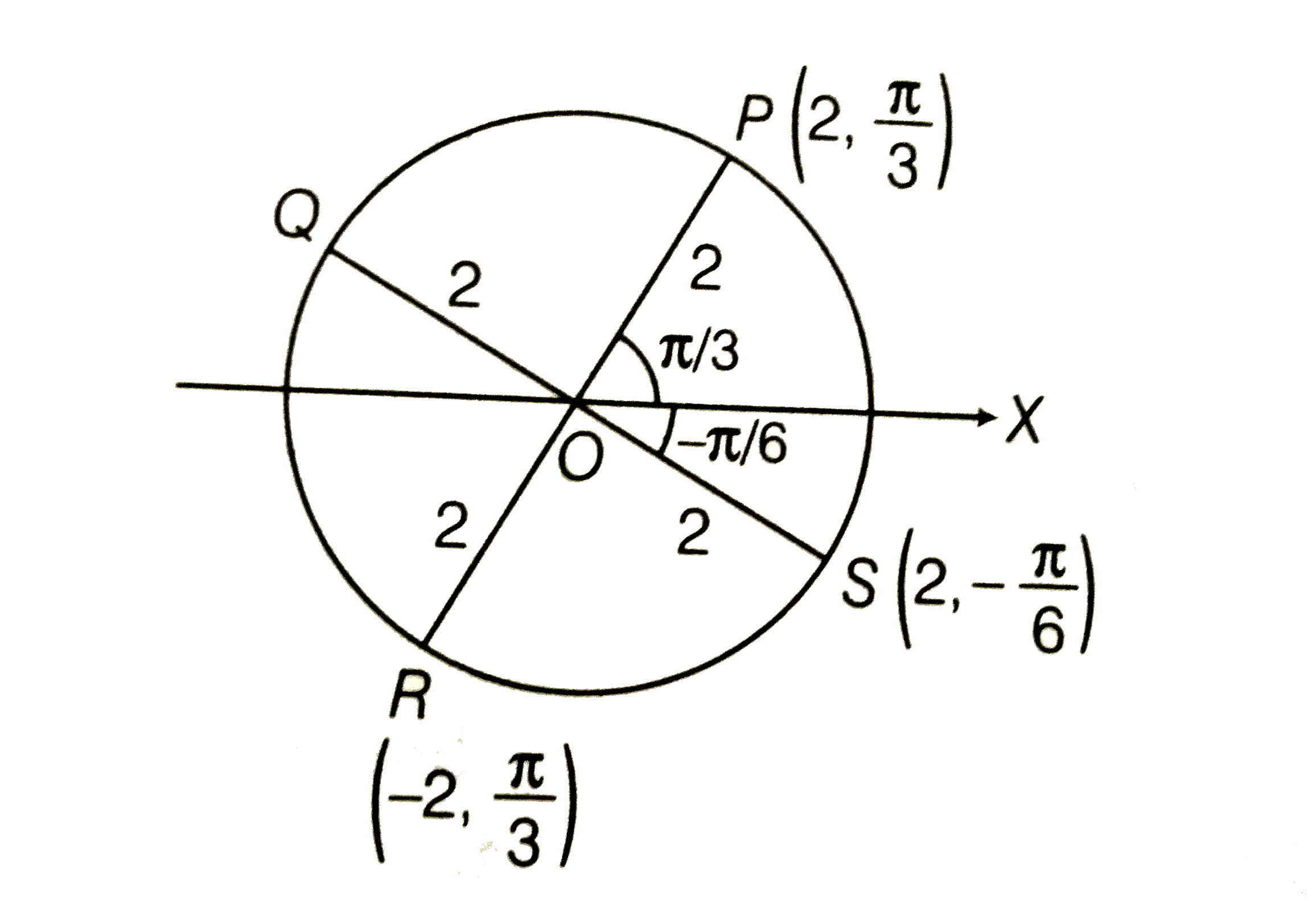
View SolutionThe cartesian coordinates of the point Q in the figure is
View SolutionConvert the following points from polar coordinates to the corresponding Cartesian coordinates.
(i) (2,π/3)
(ii) (0.π/2)
(iii) (−√2,π/4)
View SolutionFind the coordinates of the points which divide the join of the points (2-1, 3) and (4,3,1) in the ratio 3:4 internally.
View Solution
