For a man , the angle of elevation of the highest point of a tower situated west to him is 60∘ . On walking 240 meters to north , the angle of elevation reduces to 30∘ . The height of the tower is Solution in Bengali
50√3m
30√6m
60√6m
60m
Let OA the tower of height h. Also , let B amnd C be the initial and final position , respectivily , of the man .
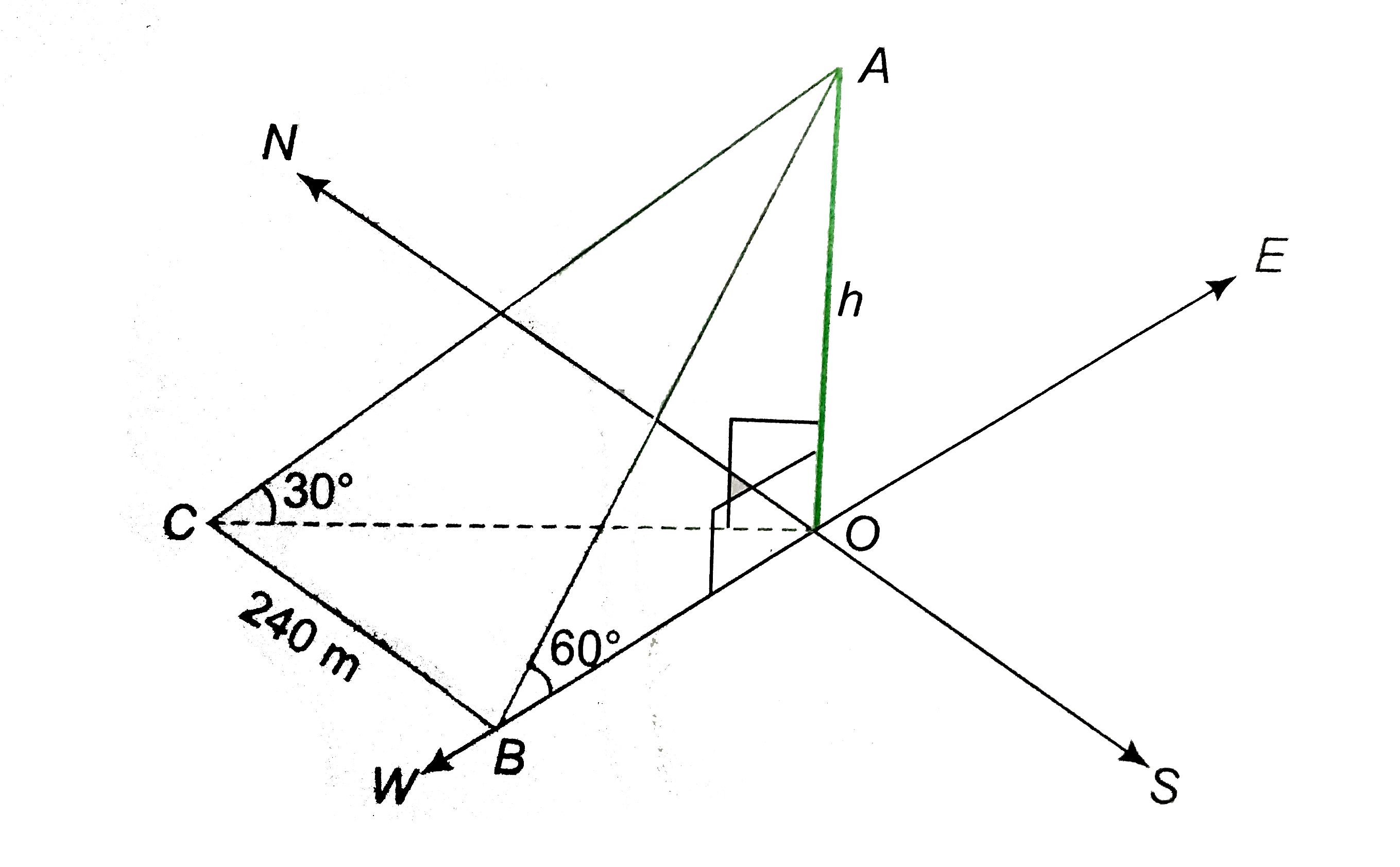
In triangle AOB ,OB =hcot60∘=h√3
in triangle AOC ,OC =hcot30∘=√3h
Now in triangle OBC ,
OB2+BC2=OC2
∴h23+(240)2=3h2
⇒8h23=(240)2
⇒h=60√6m
Topper's Solved these Questions
- HIGHT AND DISTANCE BOOK - CENGAGE PUBLICATIONCHAPTER - HIGHT AND DISTANCE EXERCISE - Archives
3 Videos
- HIGHT AND DISTANCE BOOK - CENGAGE PUBLICATIONCHAPTER - HIGHT AND DISTANCE EXERCISE - Archives
3 Videos
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercises
22 Videos
- HYPERBOLABOOK - CENGAGE PUBLICATIONCHAPTER - HYPERBOLAEXERCISE - COMPREHENSION TYPE
2 Videos
Similar Questions
A bird is sitting on the top of a vertical pole 20 m high and its elevation from a point O on the ground is 45o . It flies off horizontally straight away from the point O. After one second, the elevation of the bird from O is reduced to 30o . Then the speed (in m/s) of the bird is (1) 40(√2−1) (2) 40(√3−2) (3) 20√2 (4) 20(√3−1)
View SolutionA bird is sitting on the top of a vertical pole 20 m high and its elevation from a point O on the ground is 45o . It flies off horizontally straight away from the point O. After one second, the elevation of the bird from O is reduced to 30o . Then the speed (in m/s) of the bird is (1) 40(√2−1) (2) 40(√3−2) (3) 20√2 (4) 20(√3−1)
View SolutionDraw the graph of y= cosec 2x−cot2x. Is f(x) periodic ? If yes, what is its fundamental period ?
View SolutionThe circle x2+y2−8x=0 and hyperbola x29−y24=1 I intersect at the points A and B. Equation of a common tangent with positive slope to the circle as well as to the hyperbola is (A) 2x−√5y−20=0 (B) 2x−√5y+4=0 (C) 3x−4y+8=0 (D) 4x−3y+4=0
View SolutionFor a man , the angle of elevation of the highest point of a tower situated west to him is 60∘ . On walking 240 meters to north , the angle of elevation reduces to 30∘ . The height of the tower is
View Solutionएक मीनार के शीर्ष से सतह पर एक बिंदु A से उन्नयन कोण 30∘ है|मीनार के पाद की ओर 20 मीटर चलने पर प्राप्त बिंदु B से यह उन्नयन कोण 60∘ हो जाता है|मीनार की ऊंचाई तथा इसकी बिंदु A से दुरी ज्ञात कीजिए |
View SolutionThe angle of elevation of the top of a tower at a point A on the ground is 30^(@) . On walking 20 meters toward the tower, the angle of elevation is 60^(@) . Find the height of the tower and its distance from A.
View SolutionAt a point A, the angle of elevation of a tower is such that tangent is 512, on walking 240 m nearer the tower, the tangent of the angle of elevation is34 Then the height in m) of the tower is:
View Solutionएक मीनार के आधार से 60 मीटर दूर स्थित बिंदु पर मीनार के ऊपरी सिरे का उन्नयन कोण 30∘ है। मीनार की ऊंचाई ज्ञात कीजिये।
View SolutionThe angle of elevation of the top of a tower at a point G on the ground is 30∘. On walking 20 m towards the tower the angle of elevation becomes 60∘. The height of the tower is equal to :
View SolutionFor a man , the angle of elevation of the highest point of a tower situated west to him is 60∘ . On walking 240 meters to north , the angle of elevation reduces to 30∘ . The height of the tower is
View Solutionएक मीनार के दक्षिण की ओर बिन्दु A पर मीनार का उन्नयन कोण 45∘ तथा उत्तर की ओर स्थित बिन्दु B पर मीनार का उन्नयन कोण 45∘ हैं यदि मीनार की ऊँचाई 100 मीटर हो तो AB=
View Solutionकिसी मीनार के शिखर के मैदान पर स्थित किसी बिन्दु पर उन्नयन कोण 30∘ है। मीनार की ओर 70 मी चलने पर उन्नयन कोण 60∘ हो जाता है। मीनार की ऊँचाई क्या होगी?
View SolutionA man observes top of a tower at an angle of elevation of 30^@ . When he walked 40 m towards the tower, the angle of elevation is changed to 60^@ Find the height of the tower and distance from the first observation point to the tower.
View SolutionFor a man, the angle of elevation of the highest point of the temple situated east of him is 60∘. On walking 240 metres to north, the angle of elevation' is reduced to 30∘, then the height of the temple is
View Solution
