For a man , the angle of elevation of the highest point of a tower situated west to him is $60^{\circ}$ . On walking 240 meters to north , the angle of elevation reduces to $30^{\circ}$ . The height of the tower is

A

$50 \sqrt{3} m$

B

$30 \sqrt{6} m$

C

$60 \sqrt{6} m$

D

60m

Video Solution

Text Solution

Verified by Experts

Let OA the tower of height h. Also , let B amnd C be the initial and final position , respectivily , of the man .

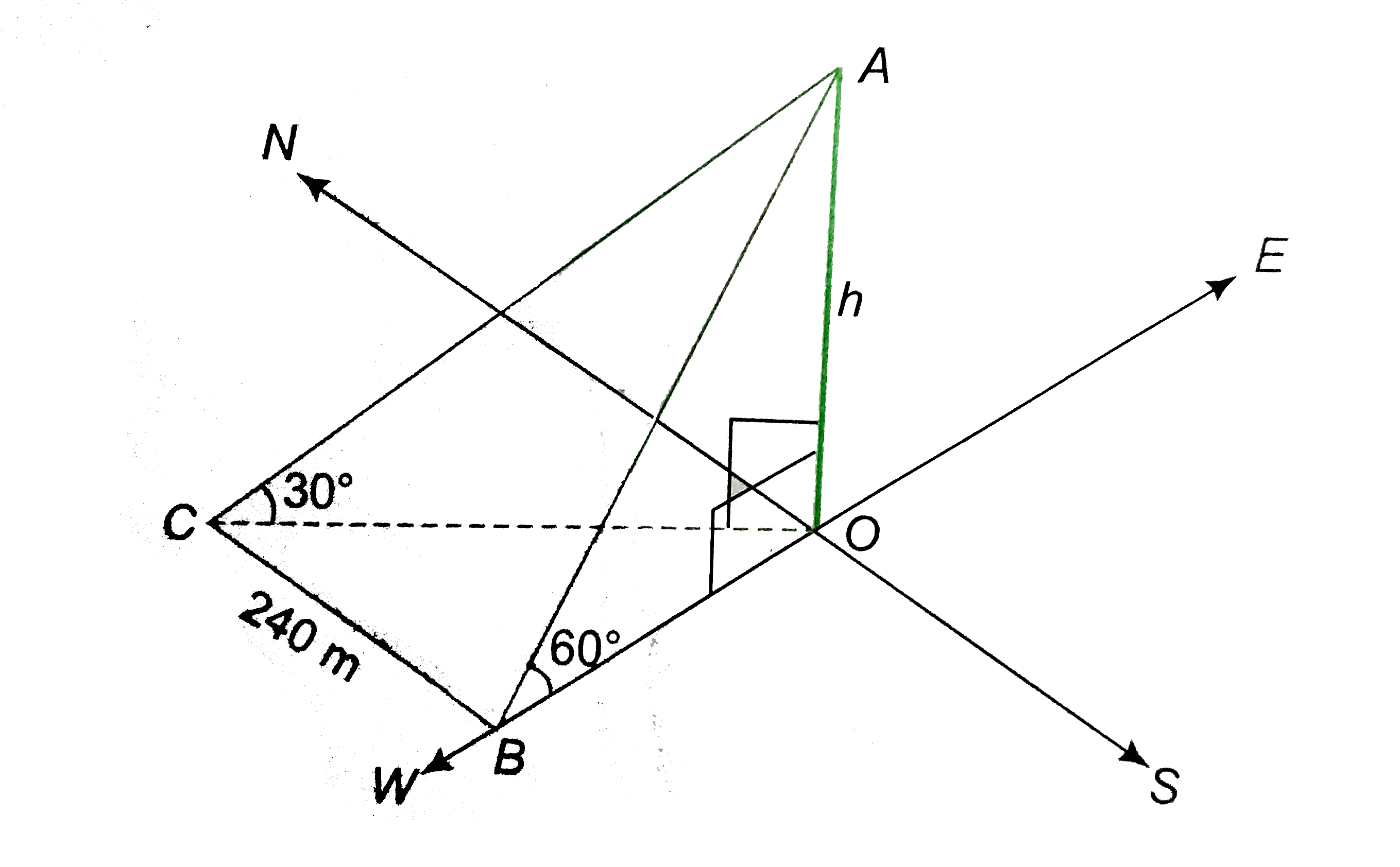
In triangle AOB ,OB = $h {cot 60}^{\circ} = \frac{h}{\sqrt{3}}$
in triangle AOC ,OC = $h {cot 30}^{\circ} = \sqrt{3} h$
Now in triangle OBC ,
$O B^{2} + B C^{2} = O C^{2}$
$∴ \frac{h^{2}}{3} + {(240)}^{2} = 3 h^{2}$
$\Rightarrow \frac{8 h^{2}}{3} = {(240)}^{2}$
$\Rightarrow h = 60 \sqrt{6} m$

|

Updated on:21/07/2023

Class 12 MATHS HIGHT AND DISTANCE

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
For a man the angle of elevation of the highest point of the temple situated east of him is $60^{\circ}$ . On walking 240 metres to north, the angle of elevation is reduced to $30^{\circ}$ .The height of the temple is
A $60 \sqrt{6} m$
B $650 m$
C $50 \sqrt{3} m$
D $30 \sqrt{6} m$
Question 2 - Select One
For a man the angle of elevation of the highest point of a temple due east of his is $60^{\circ}$ . On walking 240 metres towards north, the angle of elevation is reduced to $30^{\circ}$ . The height of the temple is
A $60 \sqrt{6} m$
B $60 m$
C $50 \sqrt{3} m$
D $30 \sqrt{3} m$
Question 3 - Select One
The angle of elevation of the top of a tower at a point G on the ground is $30^{\circ}$ . On walking 20 m towards the tower the angle of elevation becomes $60^{\circ}$ . The height of the tower is equal to :
A $10 / \sqrt{3} m$
B $20 \sqrt{3} m$
C $20 / \sqrt{3} m$
D $10 \sqrt{3} m$

CENGAGE-HIGHT AND DISTANCE -Exercise

Home
Ask Doubt
Profile