For a real number r let [r] denote the largest integer less than or eq

For a real number x let [x] denote the largest number less than or equal to x. For $x \in R$ let f (x)=[x] $sin π x$ . Then
AIf is differentiable on R.
Bf is symmetric about the line x=0
C $\int_{- 3}^{3} f (x) d x = 0$
DFor each real $α$ , the equation $f (x) - α = 0$ has infinitely many roots.
Let [x] be the greatest integer less than or equal to x, for a real number x. Then the following sum

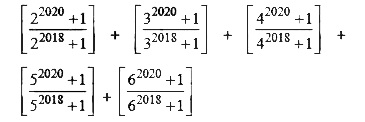
is-
A80
B85
C90
D95
For a real number x let [x] denote the largest intger less than or equal to x. The smalleset positive integer n for which the integer $\int_{1}^{n} [x] [\sqrt{x}] d x$ exceeds 60 is-
A8
B9
C10
D $[60^{2 / 3}]$

For a real number r let [r] denote the largest integer less than or equal to r. Let $a > 1$ be a real number which is not an integer and let k be the smallest positive integer positive integer such that $[a^{k}] > {[a]}^{k}$ . Then which of the following statements is always true?