For a real number x let [x] denote the largest number less than or equal to x. For x∈R let f (x)=[x] sinπx. Then
If is differentiable on R.
f is symmetric about the line x=0
∫3−3f(x)dx=0
For each real α, the equation f(x)−α=0 has infinitely many roots.
The correct Answer is:D
f(x)=[x]sinπx
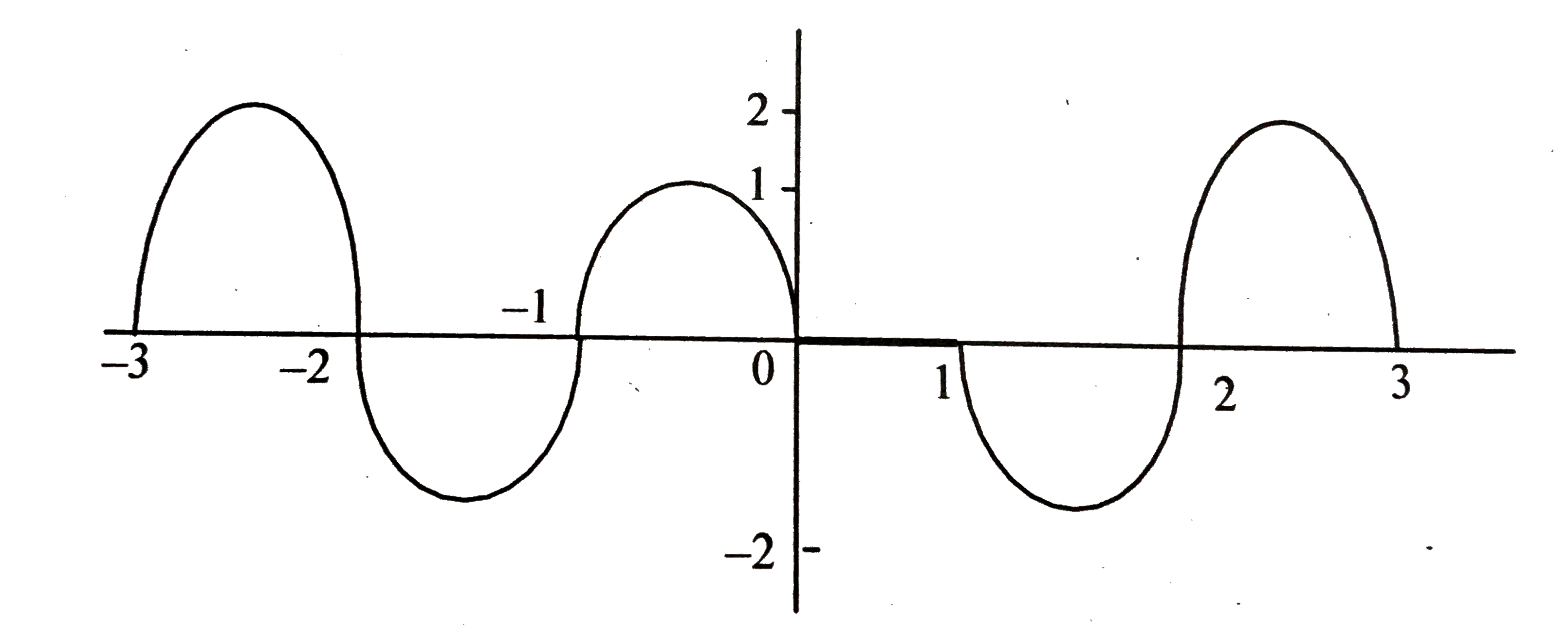
Not diff for ∀x∈R
Not sym about x=0
3∫−3f(x)dx≠0
f(x)=α will be ∞ sol"
Topper's Solved these Questions
- KVPYBOOK - KVPY PREVIOUS YEARCHAPTER - KVPYEXERCISE - PART-II MATHEMATICS
10 Videos
- KVPYBOOK - KVPY PREVIOUS YEARCHAPTER - KVPYEXERCISE - Part A - Mathematics
20 Videos
- KVPYBOOK - KVPY PREVIOUS YEARCHAPTER - KVPYEXERCISE - PART-2(MATHEMATICS)
10 Videos
- KVPY 2021BOOK - KVPY PREVIOUS YEARCHAPTER - KVPY 2021EXERCISE - PART II MATHEMATICS
4 Videos
Similar Questions
For a real number x, let [x] denote the largest integerless than or equal to x, and let {x}=x-[x]. The number ofsolutions x to the equation [x]{x}=5 with o
View SolutionFor a real number x, let [x] denote the greatest integer less than or equal to x. Let f: R→ R be defined as f(x)=2x+[x]+sinxcosx then f is
View Solution
Knowledge Check
for a real number x, let [x] denote the largest unteger less than or equal to x , and let {x} = x-[x] . The number of solution x to the equation [x] {x} =5 with 0≤x≤2015 is -
A0B3C2008D2009For any real number x, let [x]= largest integer less than or equalto x. Let f be a real valued function defined on the interval[−10,10] by
 Then, the value of (π10)2(∫10−10f(x)cosπxdx isA4B5C6D1
Then, the value of (π10)2(∫10−10f(x)cosπxdx isA4B5C6D1For a real number x let [x] denote the largest integer less than or equal to x and {x}=x−[x]. The possible integer value of n for which ∫n1[x]{x}dx exceeds 2013 is
A63B64C90D91
For any real number x, let [x] denote the largest integer less than or equal to x. If
∫100[√10xx+1]dx then the value of 9I is
View SolutionFor a real number x let [x] denote the largest integer less than or equal to x and {x}=x−[x] Let n be a positive integer. Then ∫n0cos(2π)[x]{x})dx is equal to
View SolutionFor a real number x let [x] denote the largest integer less than or equal to x and {x}=x−[x]. The possible integer value of n for which ∫n1[x]{x}dx exceeds 2013 is
View SolutionFor any real number x, let [x] denotes the largest integer less than or equal to x.Let f be a real valued function defined on the interval[-10,10] by
f(x)={(x−[x])<br>(1+[x]−x)}
Then, the value of π210∫10−10 f(x) cos π x dx is
View SolutionFor a real number x let [x] denote the largest intger less than or equal to x. The smalleset positive integer n for which the integer ∫n1[x][√x]dx exceeds 60 is-
View Solution
