From a point A(1, 1) on the circle $x^{2} + y^{2} - 4 x - 4 y + 6 = 0$ two equal chords AB and AC of length 2 units are drawn. The equation of chord BC, is

A

4x+3y-12=0

B

x+y=4

C

3x+4y=4

D

x+y=6

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

It is evident from the figure that the chord BC is

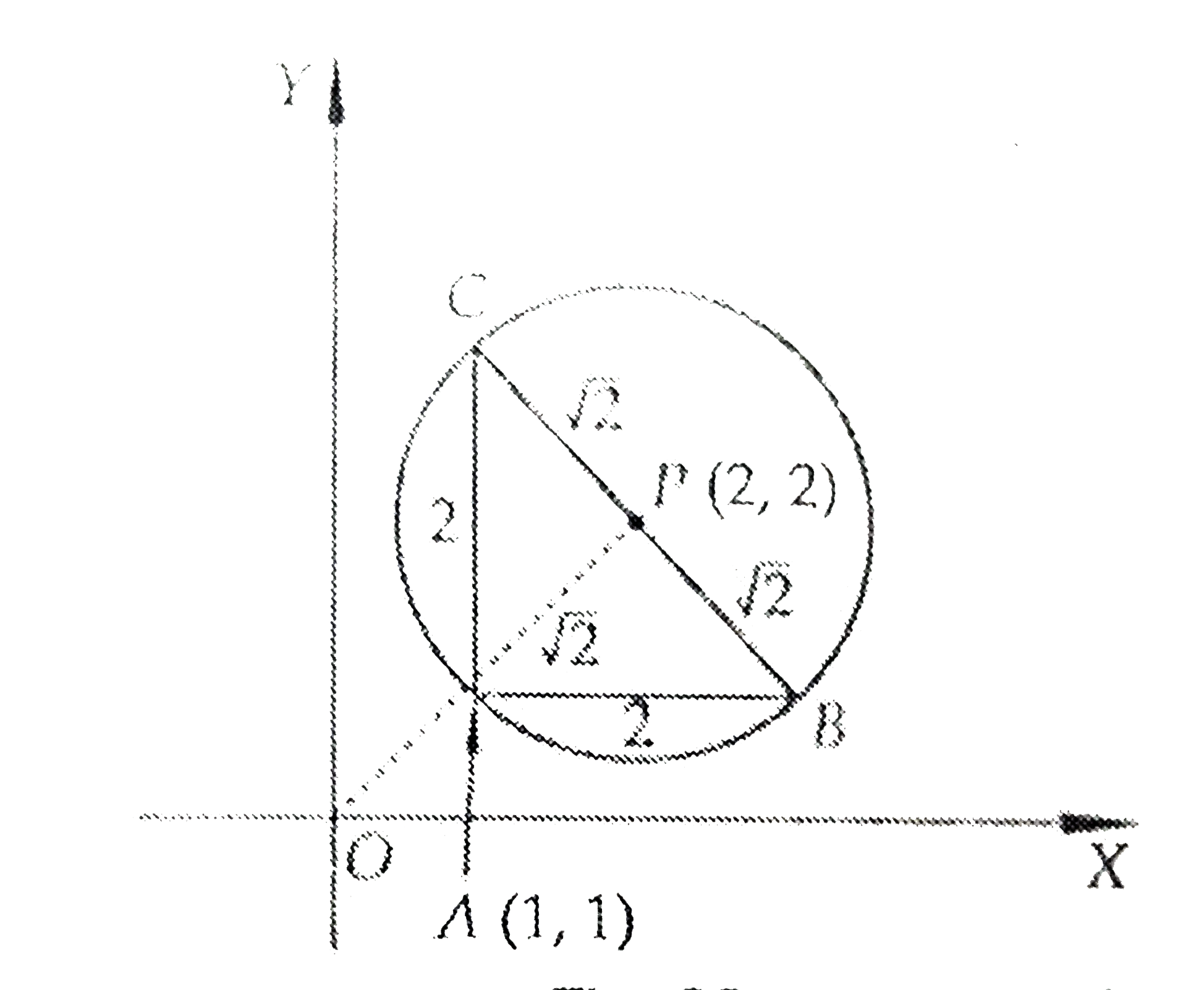
perpendicular to AP and passes through the centre P(2,2). So, its equation is x+y=4.

|

Updated on:21/07/2023

Class 12 MATHS CIRCLES

Topper's Solved these Questions

BOOK - OBJECTIVE RD SHARMACHAPTER - CIRCLESEXERCISE - Section-I (Solved MCQs)
1videos
CIRCLES
BOOK - OBJECTIVE RD SHARMACHAPTER - CIRCLESEXERCISE - Section II - Assertion Reason Type
12videos
CIRCLES
BOOK - OBJECTIVE RD SHARMACHAPTER - CIRCLESEXERCISE - Chapter Test
55videos
CIRCLES
BOOK - OBJECTIVE RD SHARMACHAPTER - CARTESIAN PRODUCT OF SETS AND RELATIONS EXERCISE - Chapter Test
31videos
CARTESIAN PRODUCT OF SETS AND RELATIONS
BOOK - OBJECTIVE RD SHARMACHAPTER - COMPLEX NUMBERS EXERCISE - Chapter Test
59videos
COMPLEX NUMBERS

Similar Questions

Knowledge Check

Question 1 - Select One
From a point P(3, 3) on the circle $x^{2} + y^{2} = 18$ , two chords PQ and PR each of 2 units length are drawn on this circle. The value of cos $(∠ Q P R)$ is equal to
A $\frac{1}{3 \sqrt{2}}$
B $- \frac{8}{9}$
C $\frac{\sqrt{2}}{3}$
D $\frac{- 4}{9}$
Question 2 - Select One
Tangents drawn from the point (4,4) to the circle
$x^{2} + y^{2} - 2 x - 2 y - 7 = 0$ meets the circle at A andB then the length of chord AB is equal to
A $2 \sqrt{3}$
B $3 \sqrt{2}$
C $4 \sqrt{3}$
D $2 \sqrt{6}$
Question 3 - Select One
If from the origin a chord is drawn to the circle $x^{2} + y^{2} - 2 x = 0$ , then the locus of the mid point of the chord has equation
A $x^{2} + y^{2} + x + y = 0$
B $x^{2} + y^{2} + 2 x + y = 0$
C $x^{2} + y^{2} - x = 0$
D $x^{2} + y^{2} - 2 x + y = 0$

OBJECTIVE RD SHARMA-CIRCLES-Section I - Solved Mcqs

Home
Ask Doubt
Profile